题目内容
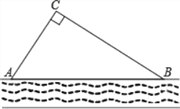
【题目】已知:如图,在△ABC中,M是边AB的中点,D是边BC延长线上的一点,且CD= ![]() BC,作DN∥CM交AC于点N.求证:四边形MCDN是平行四边形.
BC,作DN∥CM交AC于点N.求证:四边形MCDN是平行四边形. 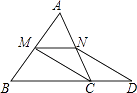
【答案】证明:取BC的中点E,连接ME. 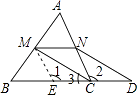
∵点M是AB的中点,点E是BC的中点,
∴ME∥AC,
∴∠1=∠2,
又 EC= ![]() BC,CD=
BC,CD= ![]() BC,
BC,
∴EC=CD,
又∵DN∥CM,
∴∠3=∠D.
在△MEC和△NCD中 ,
,
∴△MEC≌△NCD(SAS),
∴MC=ND.
又∵MC∥ND.
∴四边形MCDN是平行四边形.
【解析】直接利用全等三角形的判定与性质进而得出MC=ND,再利用平行四边形的判定方法得出答案.
【考点精析】关于本题考查的平行四边形的判定,需要了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能得出正确答案.

练习册系列答案
相关题目