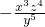题目内容
已知xy3z2是一个负数,则下列各式的值一定是正数的是( )
| A、x4y5z6 | ||
B、-
| ||
| C、-x3yz5 | ||
| D、xy2z |
分析:由已知的式子值为负数,根据非0数的平方恒大于0即z2大于0,得到x与y异号,
A、举出一个反例,满足x与y异号,但其结果为负数,比如令x=1,y=-1,z=1代入求出值,即可判定本选项不一定为正值;
B、根据x与y异号,利用两数相除,异号得负,得到
为负数,其相反数为正数,而非0数的平方恒大于0即z2大于0,即可判定其值大于0,本选项结果为正值;
C、令x=1,y=-1,z=-1代入原式,求出值为负数,本选项不一定为正值;
D、令x=1,y=-1,z=-1代入原式,求出值为负数,本选项不一定为正值.
A、举出一个反例,满足x与y异号,但其结果为负数,比如令x=1,y=-1,z=1代入求出值,即可判定本选项不一定为正值;
B、根据x与y异号,利用两数相除,异号得负,得到
| x3 |
| y5 |
C、令x=1,y=-1,z=-1代入原式,求出值为负数,本选项不一定为正值;
D、令x=1,y=-1,z=-1代入原式,求出值为负数,本选项不一定为正值.
解答:解:由xy3z2是一个负数,得到xy3z2<0,
∵z2>0,∴xy3<0,即x与y异号,
A、当x=1,y=-1,z=1,x4y5z6=-1<0,本选项不一定成立;
B、由x与y异号,得到
<0,即-
>0,又∵z4>0,
∴-
>0,本选项一定成立;
C、若x=1,y=-1,z=-1时,-x3yz5=-1<0,本选项不一定成立;
D、当x=1,y=-1,z=-1时,xy2z=-1<0,本选项不一定成立,
∴选项B中式子的值一定是正数的.
故选B
∵z2>0,∴xy3<0,即x与y异号,
A、当x=1,y=-1,z=1,x4y5z6=-1<0,本选项不一定成立;
B、由x与y异号,得到
| x3 |
| y5 |
| x3 |
| y5 |
∴-
| x3z4 |
| y5 |
C、若x=1,y=-1,z=-1时,-x3yz5=-1<0,本选项不一定成立;
D、当x=1,y=-1,z=-1时,xy2z=-1<0,本选项不一定成立,
∴选项B中式子的值一定是正数的.
故选B
点评:此题考查了有理数乘法、除法运算的取符号法则,即同号得正,异号得负,同时注意非0数的偶次幂总大于0,正数的奇次幂大于0,负数的奇次幂小于0.判断出x与y异号是解本题的关键.本题选项A,C及D利用的方法是“赋值法”,即在规定的条件下取x与y的值,利用反例的方法得到选项不一定成立.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目