题目内容
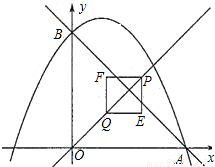
(2010•嘉兴)如图,已知抛物线y=- x2+x+4交x轴的正半轴于点A,交y轴于点B.
x2+x+4交x轴的正半轴于点A,交y轴于点B.(1)求A、B两点的坐标,并求直线AB的解析式;
(2)设P(x,y)(x>0)是直线y=x上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF,若正方形PEQF与直线AB有公共点,求x的取值范围;
(3)在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.
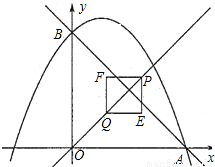
【答案】分析:(1)抛物线的解析式中,令x=0可求出B点的坐标,令y=0可求出A点的坐标,然后用待定系数法即可求出直线AB的解析式;
(2)可分别求出当点P、点Q在直线AB上时x的值,即可得到所求的x的取值范围;
(3)此题首先要计算出一个关键点:即直线AB过E、F时x的值(由于直线AB与直线OP垂直,所以直线AB同时经过E、F),此时点E的坐标为(x, ),代入直线AB的解析式即可得到x=
),代入直线AB的解析式即可得到x= ;
;
①当2≤x< 时,直线AB与PE、PF相交,设交点为C、D;那么重合部分的面积为正方形QEPF和等腰Rt△PDC的面积差,由此可得到关于S、x的函数关系式,进而可根据函数的性质及自变量的取值范围求出S的最大值及对应的x的值;
时,直线AB与PE、PF相交,设交点为C、D;那么重合部分的面积为正方形QEPF和等腰Rt△PDC的面积差,由此可得到关于S、x的函数关系式,进而可根据函数的性质及自变量的取值范围求出S的最大值及对应的x的值;
②当 ≤x≤4时,直线AB与QE、QF相交,设交点为M、N;此时重合部分的面积为等腰Rt△QMN的面积,可参照①的方法求出此时S的最大值及对应的x的值;
≤x≤4时,直线AB与QE、QF相交,设交点为M、N;此时重合部分的面积为等腰Rt△QMN的面积,可参照①的方法求出此时S的最大值及对应的x的值;
综合上述两种情况,即可比较得出S的最大值及对应的x的值.
解答:解:(1)令y=0,
得- x2+x+4=0,即x2-2x-8=0;
x2+x+4=0,即x2-2x-8=0;
解得x=-2,x=4;
所以A(4,0);
令x=0,得y=4,
所以B(0,4);
设直线AB的解析式为y=kx+b,
则有: ,
,
解得 ,故此直线的解析式为:y=-x+4;
,故此直线的解析式为:y=-x+4;
(2)当P(x,y)在直线AB上时,x=-x+4,解得x=2;
当Q( ,
, )在直线AB上时,
)在直线AB上时, =-
=- +4,解得x=4;
+4,解得x=4;
所以正方形PEQF与直线AB有公共点,且2≤x≤4;

(3)当点E(x, )在直线AB上时,
)在直线AB上时,
(此时点F也在直线AB上) =-x+4,解得x=
=-x+4,解得x= ;
;
①当2≤x< 时,直线AB分别与PE、PF有交点,
时,直线AB分别与PE、PF有交点,
设交点分别为C、D;
此时PC=x-(-x+4)=2x-4,又PD=PC,
所以S△PCD= PC2=2(x-2)2;
PC2=2(x-2)2;
S=S正方形PEQF-S△PCD=QE2-S△PCD=(x- )2-S△PCD
)2-S△PCD
从而S= x2-2(x-2)2=-
x2-2(x-2)2=- x2+8x-8=-
x2+8x-8=- (x-
(x- )2+
)2+ ;
;
因为2≤ <
< ,
,
所以当x= 时,Smax=
时,Smax= ;
;
②当 ≤x≤4时,直线AB分别与QE、QF有交点,设交点分别为M、N;
≤x≤4时,直线AB分别与QE、QF有交点,设交点分别为M、N;
此时QN=(- +4)-
+4)- =-x+4,又QM=QN,
=-x+4,又QM=QN,
所以S△QMN= QN2=
QN2= (x-4)2,
(x-4)2,
即S= (x-4)2;
(x-4)2;
当x= 时,Smax=
时,Smax= ;
;
综合①②得:当x= 时,Smax=
时,Smax= .
.
点评:此题考查了函数图象与坐标轴交点坐标的求法、一次函数解析式的确定、正方形的性质、图形面积的求法以及二次函数的应用等知识,综合性强,难度较大.
(2)可分别求出当点P、点Q在直线AB上时x的值,即可得到所求的x的取值范围;
(3)此题首先要计算出一个关键点:即直线AB过E、F时x的值(由于直线AB与直线OP垂直,所以直线AB同时经过E、F),此时点E的坐标为(x,
 ),代入直线AB的解析式即可得到x=
),代入直线AB的解析式即可得到x= ;
;①当2≤x<
 时,直线AB与PE、PF相交,设交点为C、D;那么重合部分的面积为正方形QEPF和等腰Rt△PDC的面积差,由此可得到关于S、x的函数关系式,进而可根据函数的性质及自变量的取值范围求出S的最大值及对应的x的值;
时,直线AB与PE、PF相交,设交点为C、D;那么重合部分的面积为正方形QEPF和等腰Rt△PDC的面积差,由此可得到关于S、x的函数关系式,进而可根据函数的性质及自变量的取值范围求出S的最大值及对应的x的值;②当
 ≤x≤4时,直线AB与QE、QF相交,设交点为M、N;此时重合部分的面积为等腰Rt△QMN的面积,可参照①的方法求出此时S的最大值及对应的x的值;
≤x≤4时,直线AB与QE、QF相交,设交点为M、N;此时重合部分的面积为等腰Rt△QMN的面积,可参照①的方法求出此时S的最大值及对应的x的值;综合上述两种情况,即可比较得出S的最大值及对应的x的值.
解答:解:(1)令y=0,
得-
 x2+x+4=0,即x2-2x-8=0;
x2+x+4=0,即x2-2x-8=0;解得x=-2,x=4;
所以A(4,0);
令x=0,得y=4,
所以B(0,4);
设直线AB的解析式为y=kx+b,
则有:
 ,
,解得
 ,故此直线的解析式为:y=-x+4;
,故此直线的解析式为:y=-x+4;(2)当P(x,y)在直线AB上时,x=-x+4,解得x=2;
当Q(
 ,
, )在直线AB上时,
)在直线AB上时, =-
=- +4,解得x=4;
+4,解得x=4;所以正方形PEQF与直线AB有公共点,且2≤x≤4;

(3)当点E(x,
 )在直线AB上时,
)在直线AB上时,(此时点F也在直线AB上)
 =-x+4,解得x=
=-x+4,解得x= ;
;①当2≤x<
 时,直线AB分别与PE、PF有交点,
时,直线AB分别与PE、PF有交点,设交点分别为C、D;
此时PC=x-(-x+4)=2x-4,又PD=PC,
所以S△PCD=
 PC2=2(x-2)2;
PC2=2(x-2)2;S=S正方形PEQF-S△PCD=QE2-S△PCD=(x-
 )2-S△PCD
)2-S△PCD从而S=
 x2-2(x-2)2=-
x2-2(x-2)2=- x2+8x-8=-
x2+8x-8=- (x-
(x- )2+
)2+ ;
;因为2≤
 <
< ,
,
所以当x=
 时,Smax=
时,Smax= ;
;②当
 ≤x≤4时,直线AB分别与QE、QF有交点,设交点分别为M、N;
≤x≤4时,直线AB分别与QE、QF有交点,设交点分别为M、N;此时QN=(-
 +4)-
+4)- =-x+4,又QM=QN,
=-x+4,又QM=QN,所以S△QMN=
 QN2=
QN2= (x-4)2,
(x-4)2,即S=
 (x-4)2;
(x-4)2;当x=
 时,Smax=
时,Smax= ;
;综合①②得:当x=
 时,Smax=
时,Smax= .
.点评:此题考查了函数图象与坐标轴交点坐标的求法、一次函数解析式的确定、正方形的性质、图形面积的求法以及二次函数的应用等知识,综合性强,难度较大.

练习册系列答案
相关题目
 x2+x+4交x轴的正半轴于点A,交y轴于点B.
x2+x+4交x轴的正半轴于点A,交y轴于点B.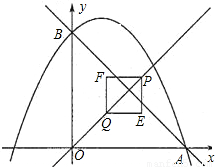
 x2+x+4交x轴的正半轴于点A,交y轴于点B.
x2+x+4交x轴的正半轴于点A,交y轴于点B.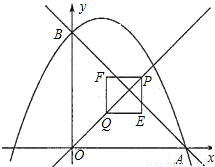
 x2+x+4交x轴的正半轴于点A,交y轴于点B.
x2+x+4交x轴的正半轴于点A,交y轴于点B.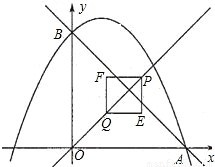
 x2+x+4交x轴的正半轴于点A,交y轴于点B.
x2+x+4交x轴的正半轴于点A,交y轴于点B.