题目内容
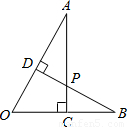
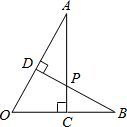 如图,AC⊥OB于点C,BD⊥OA于点D,则图中相似三角形共有
如图,AC⊥OB于点C,BD⊥OA于点D,则图中相似三角形共有
- A.3对
- B.4对
- C.5对
- D.6对
D
分析:本题可根据两角对应相等的两个三角形相似及相似三角形的传递性进行求解.
解答: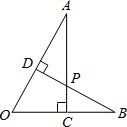
∵AC⊥OB于点C,BD⊥OA于点D,
∴∠ODB=∠ACO=90°,∠O=∠O;
∴△OCA∽△ODB,
同理可得△ADP∽△BCP∽△ACO∽△BDO.
因此本题中共有6对相似三角形.
故选D.
点评:考查相似三角形的判定定理:
(1)两角对应相等的两个三角形相似;
(2)两边对应成比例且夹角相等的两个三角形相似;
(3)三边对应成比例的两个三角形相似;
(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
分析:本题可根据两角对应相等的两个三角形相似及相似三角形的传递性进行求解.
解答:

∵AC⊥OB于点C,BD⊥OA于点D,
∴∠ODB=∠ACO=90°,∠O=∠O;
∴△OCA∽△ODB,
同理可得△ADP∽△BCP∽△ACO∽△BDO.
因此本题中共有6对相似三角形.
故选D.
点评:考查相似三角形的判定定理:
(1)两角对应相等的两个三角形相似;
(2)两边对应成比例且夹角相等的两个三角形相似;
(3)三边对应成比例的两个三角形相似;
(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,AC⊥OB于点C,BD⊥OA于点D,则图中相似三角形共有( )
如图,AC⊥OB于点C,BD⊥OA于点D,则图中相似三角形共有( ) 已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE、CD交于点O,且AO平分∠BAC.那么OB与OC相等吗?谈谈你的理由.
已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE、CD交于点O,且AO平分∠BAC.那么OB与OC相等吗?谈谈你的理由.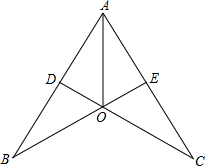 如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且AO平分∠BAC.
如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且AO平分∠BAC.