题目内容
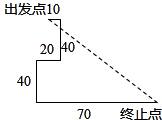 如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.求小明到达的终止点与原出发点的距离.
如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.求小明到达的终止点与原出发点的距离.
分析:根据小明在广场上只向南和向西行走,而且两个方向垂直,分别求出其实际向南所走路程和实际向西所走路程,利用勾股定理求得其终止点与源出发点之间的距离即可.
解答:解:小明实际向南走了40+40=80米,
实际向东走了10-20+70=60米,
∵正东方向与正南方向垂直,
∴终止点与原出发点的距离=
=100,
答:小明到达的终止点与原出发点的距离为100米.
实际向东走了10-20+70=60米,
∵正东方向与正南方向垂直,
∴终止点与原出发点的距离=
| 602+802 |
答:小明到达的终止点与原出发点的距离为100米.
点评:本题考查了勾股定理的应用,解题的关键是正确的求出实际向南和向东所走的路程,并利用勾股定理求解.

练习册系列答案
相关题目
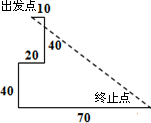 如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米,小明到达的终止点与原出发点的距离为( )米.
如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米,小明到达的终止点与原出发点的距离为( )米.| A、80 | B、100 | C、110 | D、180 |

 如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米,小明到达的终止点与原出发点的距离为米.
如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米,小明到达的终止点与原出发点的距离为米. 如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.求小明到达的终止点与原出发点的距离.
如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.求小明到达的终止点与原出发点的距离.