题目内容
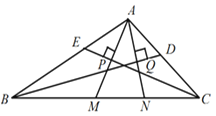
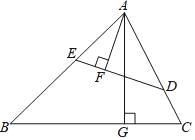
【题目】如图在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)如AF=3,AG=5,求△ADE与△ABC的周长之比.
【答案】(1)△ADE∽△ABC;(2)![]() .
.
【解析】
(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;
(2)依据△ADE∽△ABC,利用相似三角形的周长之比等于对应高之比,即可得到结论.
(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC,∴∠AED=∠ACB.
∵∠EAD=∠BAC,∴△ADE∽△ABC;
(2)由(1)可得:△ADE∽△ABC.
又∵AG⊥BC于点G,AF⊥DE于点F,∴△ADE与△ABC的周长之比=![]() =
=![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目