题目内容
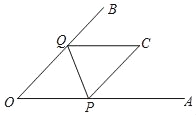
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处(点C在∠AOB的内部或一边上).
(1)当PC∥QB时,OQ= cm.
(2)当折叠后重叠部分为等腰三角形时,画出示意图,写出OQ的长.

【答案】(1)2;(2)画图见解析,OQ的长为2cm或![]() cm或2
cm或2![]() cm.
cm.
【解析】
(1)由平行线的性质得出∠O=∠CPA,由折叠的性质得出∠C=∠O,OP=CP,证出∠CPA=∠C,得出OP∥QC,证出四边形OPCQ是菱形,得出OQ=OP=2cm即可;
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有3个;依据点C在∠AOB的内部或一边上,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长.
(1)当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
故答案为:2;
(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ.
因为△CPQ是由△OPQ折叠得到,所以当△OPQ为等腰三角形时,重叠部分必为等腰三角形.
分三种情况:
①当PQ=PO时,OQ=![]() OP=2
OP=2![]() cm,
cm,

②当QO=QP时,OQ=![]() OP=
OP=![]() cm,
cm,
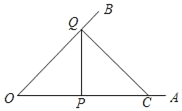
③当OQ=OP时,OQ=OP=2cm.
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或![]() cm或2
cm或2![]() cm.
cm.

练习册系列答案
相关题目