题目内容
把一枚六个面编号分别为1、2、3、4、5、6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别m,n,求二次函数y=x2+mx+n的图象与x轴只有一个交点的概率.分析:由已知可以推出即m2=4n,并且知道共有6×6种情况,通过逐步分析符合条件的只有m=2 n=1;m=4 n=4两种情况,根据以上即可求出概率.
解答:解:∵二次函数y=x2+mx+n的图象与x轴只有一个交点,
∴m2-4n=0,
即:m2=4n,
当m=1,m=3,m=5,m=6时,求的n值都不符合题意,
当m=2时,n=1符合题意,
当m=4时,n=4符合题意
即有两个符合题意,
由已知可知共有6×6种情况,
∴二次函数y=x2+mx+n的图象与x轴只有一个交点的概率是
=
.
故二次函数y=x2+mx+n的图象与x轴只有一个交点的概率是
.
∴m2-4n=0,
即:m2=4n,
当m=1,m=3,m=5,m=6时,求的n值都不符合题意,
当m=2时,n=1符合题意,
当m=4时,n=4符合题意
即有两个符合题意,
由已知可知共有6×6种情况,
∴二次函数y=x2+mx+n的图象与x轴只有一个交点的概率是
| 2 |
| 6×6 |
| 1 |
| 18 |
故二次函数y=x2+mx+n的图象与x轴只有一个交点的概率是
| 1 |
| 18 |
点评:本题考查了二次函数的性质图象,概率,列表法,树状图法等知识点,确定m n之间的关系和列树状图法是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m,n,则二次函数y=x2+mx+n的图象与x轴有两个不同交点的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
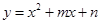 的图象与x轴有两个不同交点的概率是( ).
的图象与x轴有两个不同交点的概率是( ).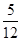 (B)
(B)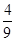 (C)
(C)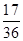 (D)
(D)