题目内容
为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三年级根据预选成绩选出了3名同学甲、乙、丙参加决赛,决赛要进行十次测试,三名选手的决赛成绩(满分为100分)如下表所示:
| 决赛成绩(单位:分) | |
| 甲 | 80 86 74 80 80 88 88 89 91 99 |
| 乙 | 85 85 87 97 85 76 88 77 87 88 |
| 丙 | 82 80 78 78 81 96 97 88 89 86 |
| 平均数 | 众数 | 中位数 | |
| 甲 | 85.5 | 87 | |
| 乙 | 85.5 | 85 | |
| 丙 | 84 |
①从平均数和众数相结合看,分析哪个同学成绩好些;
②从平均数和中位数相结合看,分析哪个同学成绩好些.
(3)如果在参加决赛的三名选手中选出1人参加市各中学总决赛,你认为哪个同学比较合适?并说明理由.
(1)平均数:85.5;众数80,78;中位数86
(2)①∵平均数都相同,乙的众数最高,∴乙的成绩好一些;
②∵平均数都相同,甲的中位数最高,∴甲的成绩好一些.
(3)应选甲,理由是:
①中位数高说明有一半次数的分数在8(7分)以上,乙和丙达不到;
②从各次考试成绩可以看出,甲对环保知识很了解,成绩从第三次后一直在进步,说明甲平时重视环保知识,并且目前正在收集学习环保知识,他的知识面也越来越广.乙和丙后阶段成绩进步不够特出.
分析:(1)平均数的计算方法是求出所有数据的和,然后除以数据的总个数.对于中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可,本题是最中间两个数的平均数.对于众数是出现次数最多的数据;
(2)可由(1)得出的表格,将三个年级的平均数,众数和中位数进行比较即可得出正确的结论;
(3)都抽取3人参加比赛,因此只需比较这三个年级前三名的成绩及其平均数即可.
点评:本题考查的是平均数、众数和中位数;弄清平均数、众数和中位数的定义和它们之间的区别是解题的关键.
(2)①∵平均数都相同,乙的众数最高,∴乙的成绩好一些;
②∵平均数都相同,甲的中位数最高,∴甲的成绩好一些.
(3)应选甲,理由是:
①中位数高说明有一半次数的分数在8(7分)以上,乙和丙达不到;
②从各次考试成绩可以看出,甲对环保知识很了解,成绩从第三次后一直在进步,说明甲平时重视环保知识,并且目前正在收集学习环保知识,他的知识面也越来越广.乙和丙后阶段成绩进步不够特出.
分析:(1)平均数的计算方法是求出所有数据的和,然后除以数据的总个数.对于中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可,本题是最中间两个数的平均数.对于众数是出现次数最多的数据;
(2)可由(1)得出的表格,将三个年级的平均数,众数和中位数进行比较即可得出正确的结论;
(3)都抽取3人参加比赛,因此只需比较这三个年级前三名的成绩及其平均数即可.
点评:本题考查的是平均数、众数和中位数;弄清平均数、众数和中位数的定义和它们之间的区别是解题的关键.

练习册系列答案
相关题目
6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环 保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:
| 分 组 | 频数 | 频率 |
| 49.5~59.5 | | 0.08 |
| 59.5~69.5 | | 0.12 |
| 69.5~79.5 | 20 | |
| 79.5~89.5 | 32 | |
| 89.5~100.5 | | a |
(1)直接写出a的值,并补全频数分布直方图.
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
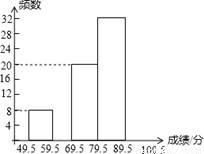
6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环 保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:
|
分 组 |
频数 |
频率 |
|
49.5~59.5 |
|
0.08 |
|
59.5~69.5 |
|
0.12 |
|
69.5~79.5 |
20 |
|
|
79.5~89.5 |
32 |
|
|
89.5~100.5 |
|
a |
(1)直接写出a的值,并补全频数分布直方图.
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?