题目内容
【题目】在△ABC中，AB＝13 cm，AC＝20 cm，BC 边上的高为12 cm，求△ABC 的面积．
【答案】126 cm2或66 cm2
【解析】试题分析：
分两种情况：①∠B为锐角；②∠B为钝角；利用勾股定理求出BD、CD，即可求出BC的长．
试题解析：
当∠B 为锐角时(图①),
在Rt△ABD中，
BD＝
＝5(cm).
在Rt△ADC中，
CD＝
＝16(cm).
∴BC＝BD＋CD＝5＋16＝21(cm).
∴S△ABC＝
BC·AD＝
×21×12＝126(cm2).
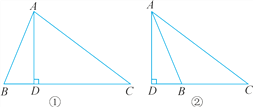
当∠B 为钝角时(图②),
同理，BC＝CD－BD＝16－5＝11(cm)．
∴S△ABC＝
BC·AD＝
×11×12＝66(cm2)．
∴△ABC 的面积为126 cm2或66 cm2 .
练习册系列答案
相关题目
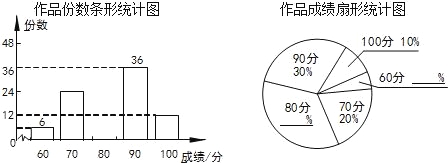
【题目】某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%，20%，30%的比例计入学期总评成绩，90分以上为优秀．甲、乙、丙三人的各项成绩如下表（单位：分），学期总评成绩优秀的是（ ）
纸笔测试 | 实践能力 | 成长记录 | |
甲 | 90 | 83 | 95 |
乙 | 88 | 90 | 95 |
丙 | 90 | 88 | 90 |
A. 甲 B. 乙、丙 C. 甲、乙 D. 甲、丙
