题目内容
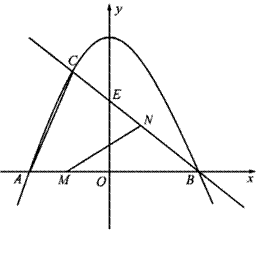
如图,抛物线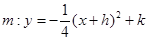 与
与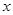 轴的交点为A、B,与
轴的交点为A、B,与 轴的交点为C,顶点为
轴的交点为C,顶点为 ,将抛物线
,将抛物线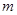 绕点B旋转
绕点B旋转 ,得到新的抛物线
,得到新的抛物线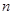 ,它的顶点为D.
,它的顶点为D.
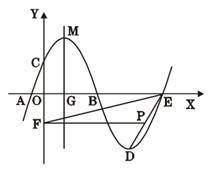
(1)求抛物线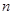 的解析式;
的解析式;
(2)设抛物线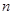 与
与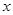 轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为
轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为 ,△PEF的面积为S,求S与
,△PEF的面积为S,求S与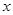 的函数关系式,写出自变量
的函数关系式,写出自变量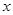 的取值范围;
的取值范围;
(3)设抛物线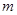 的对称轴与
的对称轴与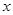 轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
【答案】
(1)抛物线n的解析式为 (2)S=
(2)S= (3)直线CM与⊙G相切;证明
(3)直线CM与⊙G相切;证明 所以直线CM与⊙G相切
所以直线CM与⊙G相切
【解析】
试题分析:(1)∵抛物线m的顶点为 ,∴m的解析式为:
,∴m的解析式为:
解方程: 得:x1="
-2" ,x2=8 ∴
得:x1="
-2" ,x2=8 ∴
∵抛物线n是由抛物线m绕点B旋转 得到,∴D的坐标为
得到,∴D的坐标为
∴抛物线n的解析式为: ,即
,即
(2)∵点E与点A关于点B中心对称,∴E , 设直线ED的解析式为
, 设直线ED的解析式为 ,
,
则 ,解得
,解得 ∴直线ED的解析式为
∴直线ED的解析式为
又点P的坐标为 ,∴S=
,∴S= =–
=– xy=
xy=
即S=
(3)直线CM与⊙G相切
理由如下:∵抛物线m的解析式为y= ,令
,令 得
得 .∴
.∴
∵抛物线m的对称轴与 轴的交点为G,∴OC=4,OG=3,
轴的交点为G,∴OC=4,OG=3, ∴由勾股定理得CG=5
∴由勾股定理得CG=5
又∵AB=10,∴⊙G的半径为5,∴点C在⊙G上

过M点作y轴的垂线,垂足为N,则
又 ,
,
∴
 ∴根据勾股定理逆定理,得∠GCM=900
∴根据勾股定理逆定理,得∠GCM=900
∴ ∴直线CM与⊙G相切
∴直线CM与⊙G相切
考点:抛物线,勾股定理,直线与圆相切
点评:本题考查抛物线,勾股定理,直线与圆相切,要求考生掌握用待定系数法求函数的解析式,会判定直线与圆相切,熟悉勾股定理的内容

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 .]
.] 
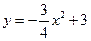 与
与 轴交于点
轴交于点 、点
、点 ,与直线
,与直线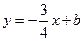 相交于点
相交于点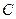 ,直线
,直线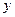 轴交于点
轴交于点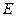 。
。
 的解析式;
的解析式; 的面积;
的面积; 在线段
在线段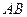 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从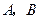 重合),同时,点
重合),同时,点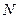 在射线
在射线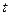 秒,请写出
秒,请写出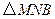 的面积
的面积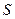 与
与 与
与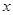 轴交于
轴交于 两点,于
两点,于 轴交于点
轴交于点 ,
,
 ;
; ,使四边形
,使四边形 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点 与
与 轴交于A、B两点,与y轴交于C点,且
轴交于A、B两点,与y轴交于C点,且 .
.
 是
是 值最小
值最小 的值.
的值.