题目内容
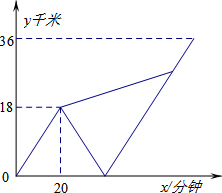 甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)电动车的速度为______千米/分钟;
(2)甲步行所用的时间为______分;
(3)求乙返回到学校时,甲与学校相距多远?
解:(1)由图象,得
18÷20=0.9
故答案为:0.9;
(2)乙从学校追上甲所用的时间为:(36-13.5)÷0.9=25分钟,
∴甲步行所用的时间为:20+25=45分钟.
故答案为:45;
(3)由题意,得
甲步行的速度为:(36-13.5-18)÷45=0.1.
乙返回到学校时,甲与学校的距离为:18+0.1×20=20.
答:乙返回到学校时,甲与学校相距20km.
分析:(1)根据图象由速度=路程÷时间就可以求出结论;
(2)先求出乙追上甲所用的时间,再加上乙返回学校所用的时间就是乙步行所用的时间.
(3)先根据第二问的结论求出甲步行的速度,就可以求出乙回到学校时,甲与学校的距离.
点评:本题考查了速度=路程÷时间的运用,追击问题的运用,解答本题时认真分析函数图象反应的数量关系是关键.
18÷20=0.9
故答案为:0.9;
(2)乙从学校追上甲所用的时间为:(36-13.5)÷0.9=25分钟,
∴甲步行所用的时间为:20+25=45分钟.
故答案为:45;
(3)由题意,得
甲步行的速度为:(36-13.5-18)÷45=0.1.
乙返回到学校时,甲与学校的距离为:18+0.1×20=20.
答:乙返回到学校时,甲与学校相距20km.
分析:(1)根据图象由速度=路程÷时间就可以求出结论;
(2)先求出乙追上甲所用的时间,再加上乙返回学校所用的时间就是乙步行所用的时间.
(3)先根据第二问的结论求出甲步行的速度,就可以求出乙回到学校时,甲与学校的距离.
点评:本题考查了速度=路程÷时间的运用,追击问题的运用,解答本题时认真分析函数图象反应的数量关系是关键.

练习册系列答案
相关题目
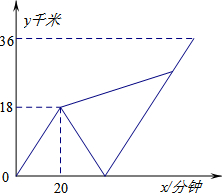 (2013•吉林)甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(2013•吉林)甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题: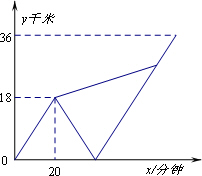

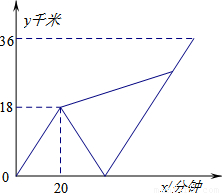 甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题: