题目内容
【题目】如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF,试说明这是中心对称图形.
【答案】解:连接CD,交AB于O.
∵在△ACO与△BDO,
∴△ACO≌△BDO(AAS),
故OA=OB,OC=OD.
∵DE∥CF,
∴∠DEO=∠CFO,
在△ODE和△OCF中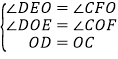
∴△ODE≌△OCF(AAS),
所以OE=OF,是中心对称图形.
【解析】连接CD,通过证明OA=OB,OC=OD,OE=OF,再根据中心对称图形的概念进行判断.
【考点精析】本题主要考查了中心对称及中心对称图形的相关知识点,需要掌握如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目