题目内容
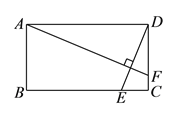
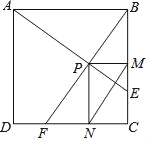
【题目】已知:如图,等腰![]() 中,
中,![]() ,
,![]() ∥
∥![]() ,CD∥
,CD∥![]() ,点
,点![]() 沿着
沿着![]() 从
从![]() 向
向![]() 运动,同时点
运动,同时点![]() 沿着
沿着![]() 从
从![]() 向
向![]() 运动,
运动,![]() 、
、![]() 两点速度相同,当
两点速度相同,当![]() 到达
到达![]() 时,两点停止运动.
时,两点停止运动.

(1)图中有__________对全等三角形.请你找一对说明理由,写出过程.
(2)在![]() 、
、![]() 运动过程中,图中阴影部分的面积是否发生变化?请说明理由.
运动过程中,图中阴影部分的面积是否发生变化?请说明理由.
(3)当![]() 平分
平分![]() 时,延长
时,延长![]() 交
交![]() 于
于![]() ,试说明
,试说明![]() .
.
(4)在(3)的条件下,若![]() ,请问此时
,请问此时![]() 点和
点和![]() 点重合吗?为什么?
点重合吗?为什么?
【答案】(1)3,见解析;(2)图中阴影部分的面积不发生变化,理由见解析;(3)见解析;(4)E点和G点重合,理由见解析.
【解析】
(1)根据全等三角形的判定定理写出图中的所有全等三角形,根据SAS定理证明△ABC≌△CDA;
(2)证明△BCE≌△DAF,得到图中阴影部分的面积=△ABC的面积;
(3)利用SAS定理证明△AEC≌△CFD,根据全等三角形的性质解答;
(4)根据等腰三角形的判定定理得到EA=EC,根据△BCE≌△GCF得到BC=GC,证明CB=CE,证明结论.
解:(1)△ABC≌△CDA,△BCE≌△DAF,△AEC≌△CFD,
证明△ABC≌△CDA,
证明:∵AD∥BC,CD∥AB,
∴四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠ADC,
在△ABC和△CDA中,AB=CD,∠B=∠ADC,BC=AD,
∴△ABC≌△CDA(SAS),
故答案为:3;
(2)在E、F运动过程中,图中阴影部分的面积不发生变化,
理由:由题意得,BE=AF,
∵AB=AC,
∴∠ABC=∠ACB,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DAC=∠B,
在△BCE和△DAF中,BE=AF,∠B=∠DAF,BC=DA,
∴△BCE≌△DAF(SAS),
∴图中阴影部分的面积=△ABC的面积,
∴在E、F运动过程中,图中阴影部分的面积不发生变化;
(3)∵BE=AF,
∴AE=CF,
在△AEC和△CFD中,AE=CF,∠CAE=∠DCF,AC=DC,
∴△AEC≌△CFD(SAS)
∴∠AEC=∠DFC,
∴∠BEC=∠GFC,
∵∠BCE=∠ACE,
∴∠CGF=∠B;
(4)∵AB∥CD,
∴∠BAC=∠ACD,
∵∠ECA=∠ACD,
∴∠ECA=∠BAC,
∴EA=EC,
∵CF=AE,
∴CF=CE,
在△BCE和△GCF中,∠BCE=∠GCF,∠B=∠CGF,CE=CF,
∴△BCE≌△GCF(AAS)
∴BC=GC,
∵∠EAC=∠ECA,∠BCE=∠ACE,
∴∠BEC=∠ACB,
∵∠ACB=∠B,
∴∠BEC=∠B,
∴CB=CE,又CB=GC,
∴E点和G点重合.

 小学课时特训系列答案
小学课时特训系列答案