Question

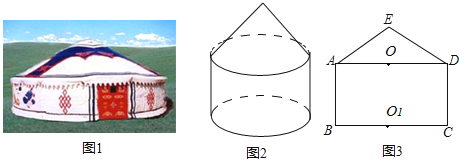
【题目】图（1）是一个蒙古包的照片，这个蒙古包可以近似看成是圆锥和圆柱组成的几何体，如图（2）所示．

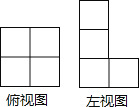
（1）请画出这个几何体的俯视图；

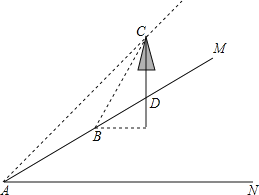
（2）图（3）是这个几何体的正面示意图，已知蒙古包的顶部离地面的高度EO1=6米，圆柱部分的高OO1=4米，底面圆的直径BC=8米，求∠EAO的度数（结果精确到0.1°）．

Answer 1

【答案】（1）见解析；（2）26.6°

【解析】

试题分析：（1）根据图2，画出俯视图即可；

（2）连接EO1，如图所示，由EO1﹣OO1求出EO的长，由BC=AD，O为AD中点，求出OA的长，在直角三角形AOE中，利用锐角三角函数定义求出tan∠EAO的值，即可确定出∠EAO的度数．

解：（1）画出俯视图，如图所示：

（2）连接EO1，如图所示：

∵EO1=6米，OO1=4米，

∴EO=EO1﹣OO1=6﹣4=2米，

∵AD=BC=8米，

∴OA=OD=4米，

在Rt△AOE中，tan∠EAO===，

则∠EAO≈26.6°．