Question

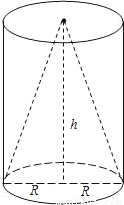
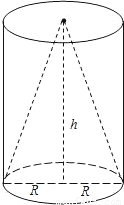
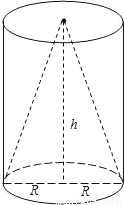
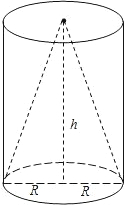如图，同底等高的圆锥和圆柱，它们的底面直径与高相等（2R=h），那么圆锥和圆柱的侧面积比为

 

．

Answer 1

分析：利用圆锥的高，母线长，底面半径组成直角三角形可求得圆锥母线长；圆锥的侧面积=底面周长×母线长÷2；表面积=侧面积+两个底面积=底面周长×高+2πr²．代入计算比较即可．

解答：解：底面直径与高相等（2R=h），由勾股定理得，圆锥的母线长=

5

R，由底面周长=2πR，圆柱的侧面面积=2πR×2R=4πR²，圆锥的侧面面积=

1

2

×2πR×

5

R=

5

πR²，
∴圆锥和圆柱的侧面积比为

5

：4．

点评：本题利用了圆柱的侧面面积公式，勾股定理，圆的周长公式和扇形的面积公式求解．