题目内容
【题目】如图,在△ABC中,AB=AC=6,∠BAC=120,以A为顶点的的等边三角形ADE绕点A在∠BAC内旋转,AD、AE与BC边分别交于点F、G若点B关于直线AD的对称点为M,MG⊥BC,则BF的长为____________.

【答案】![]()
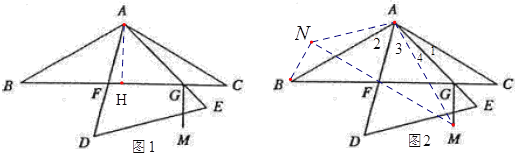
【解析】作AH⊥BC于H,如图1,
∵AB=AC=6,∠BAC=120°,
∴∠B=30°,BH=CH,
在Rt△ABH中,AH=![]() AB=3,BH=
AB=3,BH=![]() AH=3
AH=3![]() ,,
,,
∴BC=2BH=6![]() ,
,
把△ACG绕点A顺时针旋转120°得到△ABN,连结FN、AM,FM,如图2,
则BN=CG,AG=AG,∠ABN=∠C=30°,∠1=∠BAN,
∴∠FBN=60°,
∵∠FAG=60°,
∴∠1+∠2=60°,
∴∠FAN=60°,
在△AFG和△AFN中, 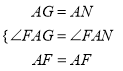 ,
,
∴△AFG≌△AFN,
∴FG=FN,
∵点B关于直线AD的对称点为M,
∴FB=FM,AB=AM,∠2=∠3,
而∠3+∠4=60°,∠1+∠2=60°,
∴∠1=∠4,
而AC=AB=AM,
∴△AMG与△ACG关于AG对称,
∴GM=GC,
∴GM=BN,
在△FMG和△FBN中, 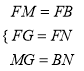 ,
,
∴△FMG≌△FBN,
∴∠FGM=∠BNF=90°,
在Rt△BFN中,∵∠FBN=60°,∴BN=![]() BF,FN=
BF,FN=![]() BF,
BF,
∴CG=![]() BF,FG=
BF,FG=![]() BF,
BF,
∴BF+![]() BF+
BF+![]() BF=BC=6
BF=BC=6![]() ,
,
∴BF=6![]() -6,
-6,
故答案为:6![]() -6.
-6.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目



