题目内容
在位于O处某海防哨所的北偏东60°相距6海里的A处,有一艘快艇正向正南方向航行,经过一段时间快艇到达哨所东南方向的B处,则A、B间的距离是 海里.(精确到0.1海里,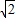 ≈1.414,
≈1.414,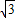 ≈1.732)
≈1.732)
【答案】分析:在直角△AOD中,根据AO和∠AOD的正切函数,先求出OD和AD.再把OD放到直角△OBD中,利用45°角的正切值求出BD,最后相加即可.
解答: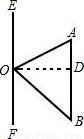 解:如图,∠EOA=60°,∠FOB=45°,OA=6.
解:如图,∠EOA=60°,∠FOB=45°,OA=6.
过点O作OD⊥AB于点D.
∵∠EOA=60°,
∴∠AOD=30°.
∴AD=3,OD=3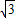 .
.
∵∠FOB=45°,
∴∠BOD=45°.
∴OD=BD=3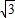 .
.
∴AB=AD+BD=3+3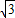 ≈8.2.
≈8.2.
∴A、B间的距离是8.2海里.
点评:解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
解答:
 解:如图,∠EOA=60°,∠FOB=45°,OA=6.
解:如图,∠EOA=60°,∠FOB=45°,OA=6.过点O作OD⊥AB于点D.
∵∠EOA=60°,
∴∠AOD=30°.
∴AD=3,OD=3
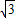 .
.∵∠FOB=45°,
∴∠BOD=45°.
∴OD=BD=3
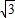 .
.∴AB=AD+BD=3+3
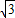 ≈8.2.
≈8.2.∴A、B间的距离是8.2海里.
点评:解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
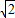 ≈1.414,
≈1.414,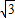 ≈1.732)
≈1.732)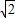 ≈1.414,
≈1.414,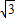 ≈1.732)
≈1.732)