题目内容
已知：如图，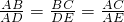
且B、D、E三点在一直线，求证：∠BAD=∠CAE．
解：∵，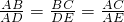
∴△ADE∽△ABC，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
∴∠BAD=∠CAE．
分析：根据已知得出△ADE∽△ABC，进而得出∠BAC=∠DAE，即可得出答案．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出△ADE∽△ABC是解决问题的关键．
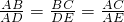，∴△ADE∽△ABC，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
∴∠BAD=∠CAE．
分析：根据已知得出△ADE∽△ABC，进而得出∠BAC=∠DAE，即可得出答案．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出△ADE∽△ABC是解决问题的关键．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
内交于点C，且S△AOC=6．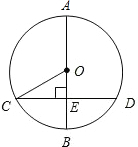
已知：如图，AB是⊙O的直径，CD是⊙O的弦，且AB⊥CD，垂足为E，连接OC，OC=5，CD=8，求BE的长．
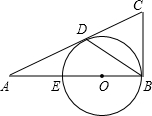与AC切于D，且AD=2，AE=1．
且B、D、E三点在一直线，求证：∠BAD=∠CAE．