Question

已知：三角形ABC内接于⊙O，过点A作直线EF．
（1）如图1，AB为直径，要使得EF是⊙O的切线，还需添加的条件是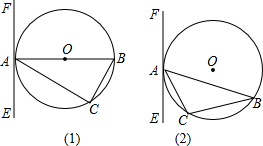？（只须写出三种情况）
（2）如图2，AB为非直径的弦，∠CAE=∠B，求证：EF是⊙O的切线．

Answer 1

（1）解：①∠CAE=∠B，
②AB⊥FE，
③∠BAC+∠CAE=90°（或∠BAC与∠CAE互余），
④∠C=∠FAB，
⑤∠EAB=∠FAB，
任选三个即可．

（2）证明：连接AO并延长AO交⊙O于H，连接HC；
∴∠H=∠B，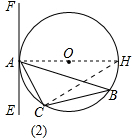
∵AH是直径，
∴∠ACH=90°．
∵∠B=∠CAE，
∴∠CAE+∠HAC=90°，
∴HA⊥EF．
∵OA是⊙O的半径，
∴EF是⊙O的切线．
分析：（1）要使得EF是⊙O的切线，只需有EF⊥AB即可；因此添加的条件能够得出EF⊥AB即可．
（2）连接AO并延长AO交⊙O于H，连接HC；根据角与角的相等及互余关系，可得HA⊥EF；故EF是⊙O的切线．
点评：本题考查的是切线的判定与应用，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．