题目内容
已知:如图,有一飞行中的热气球,在A处时的热气球的探测器显示,从热气球看正前方一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,热气球离地面的高度为150米,为了安全,避免热气球撞上高楼,请问热气球此时至少应再上升多少米?(注:
 ≈1.732,结果精确到1米)
≈1.732,结果精确到1米)
【答案】分析:首先分析图形:根据题意构造直角三角形;本题涉及多个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
解答:解:如图,在△BDA中,∵∠BAD=45°,∠ADB=90°
∴∠ABD=45°
∴BD=AD
在Rt△ADC中,∵∠ADC=90°,∠DAC=60°
∴∠ACD=30°
∵CD=150
∴AD=CD•tan30°=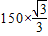 ≈50×1.732≈87
≈50×1.732≈87
即BD≈87.
答:热气球此时至少应再上升87米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
解答:解:如图,在△BDA中,∵∠BAD=45°,∠ADB=90°
∴∠ABD=45°
∴BD=AD
在Rt△ADC中,∵∠ADC=90°,∠DAC=60°
∴∠ACD=30°
∵CD=150
∴AD=CD•tan30°=
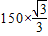 ≈50×1.732≈87
≈50×1.732≈87即BD≈87.
答:热气球此时至少应再上升87米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
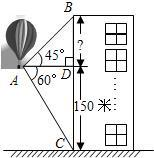 已知:如图,有一飞行中的热气球,在A处时的热气球的探测器显示,从热气球看正前方一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,热气球离地面的高度为150米,为了安全,避免热气球撞上高楼,请问热气球此时至少应再上升多少米?
已知:如图,有一飞行中的热气球,在A处时的热气球的探测器显示,从热气球看正前方一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,热气球离地面的高度为150米,为了安全,避免热气球撞上高楼,请问热气球此时至少应再上升多少米? ≈1.732,结果精确到1米)
≈1.732,结果精确到1米)
 ≈1.732,结果精确到1米)
≈1.732,结果精确到1米)
 ≈1.732,结果精确到1米)
≈1.732,结果精确到1米)