题目内容
 如图,D、E、F为△ABC三边的中点,且S△DEF=1,则S△ABC的面积为
如图,D、E、F为△ABC三边的中点,且S△DEF=1,则S△ABC的面积为
- A.2
- B.3
- C.4
- D.6
C
分析:由于D、E、F为△ABC三边的中点,根据中位线定理得到△DEF的三边分别是△ABC的三边的一半,由此得到△DEF∽△ABC,然后利用相似三角形的性质即可解决问题.
解答:∵D、E、F为△ABC三边的中点,
∴BC=2EF、AB=2DE、AC=2DF,
∴△DEF∽△ABC,
∴S△DEF:S△ABC=( )2,
)2,
而S△DEF=1,
∴S△ABC的面积为4.
故选C.
点评:此题主要考查了相似三角形的性质与判定,也利用了中位线定理,首先利用中位线定理构造相似条件证明相似,然后利用相似三角形的性质即可解决问题.
分析:由于D、E、F为△ABC三边的中点,根据中位线定理得到△DEF的三边分别是△ABC的三边的一半,由此得到△DEF∽△ABC,然后利用相似三角形的性质即可解决问题.
解答:∵D、E、F为△ABC三边的中点,
∴BC=2EF、AB=2DE、AC=2DF,
∴△DEF∽△ABC,
∴S△DEF:S△ABC=(
 )2,
)2,而S△DEF=1,
∴S△ABC的面积为4.
故选C.
点评:此题主要考查了相似三角形的性质与判定,也利用了中位线定理,首先利用中位线定理构造相似条件证明相似,然后利用相似三角形的性质即可解决问题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

 25、如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.
25、如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.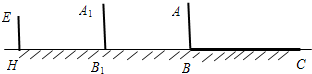
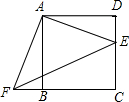 如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.
如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.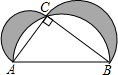 如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是
如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是