题目内容
 如图所示,在长为9,宽为8的矩形纸片上紧贴三条边剪下一个圆,在剩在纸片上如果再剪两上小圆⊙O1与⊙O2,那么这两个小圆的最大直径d=
如图所示,在长为9,宽为8的矩形纸片上紧贴三条边剪下一个圆,在剩在纸片上如果再剪两上小圆⊙O1与⊙O2,那么这两个小圆的最大直径d=2
2
.分析:要求校园的最大直径,由题意知大圆半径为4,那么连接OO1,OO2,O1O2,
设大圆半径为R,小圆半径为r,用R、r分别表示
OO1=OO2=R+r=4+r,OP=9-4-r.O1O2=8-2r
再由勾股定理得r1=1,r2=25(舍去),
所以半径r=1,则直径为2
设大圆半径为R,小圆半径为r,用R、r分别表示
OO1=OO2=R+r=4+r,OP=9-4-r.O1O2=8-2r
再由勾股定理得r1=1,r2=25(舍去),
所以半径r=1,则直径为2
解答:
解:如图,连接OO1,OO2,O1O2
设大圆半径为R,小圆半径为r,P是O1O2的中点,
∵⊙O是在长为9,宽为8的矩形纸片上紧贴三条边剪下一个圆,
∴R=4,OO1=OO2=R+r=4+r,OP=9-4-r.O1O2=8-2r
∵OP⊥O1O2
∴OP2+PO12=OO12.
即(5-r)2+(4-r)2=(4+r)2
∴r1=1,r2=25(舍去),
∴最大直径d=2r=2.

解:如图,连接OO1,OO2,O1O2
设大圆半径为R,小圆半径为r,P是O1O2的中点,
∵⊙O是在长为9,宽为8的矩形纸片上紧贴三条边剪下一个圆,
∴R=4,OO1=OO2=R+r=4+r,OP=9-4-r.O1O2=8-2r
∵OP⊥O1O2
∴OP2+PO12=OO12.
即(5-r)2+(4-r)2=(4+r)2
∴r1=1,r2=25(舍去),
∴最大直径d=2r=2.
点评:这道题考查了相切圆的性质和矩形性质,以及同学们的作图能力,同学们应熟练掌握.

练习册系列答案
相关题目
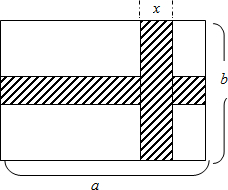 如图所示,在长为a cm,宽为b cm的长方形地面上修两条同样宽的道路,余下部分作为绿化地,若设路宽为x cm.
如图所示,在长为a cm,宽为b cm的长方形地面上修两条同样宽的道路,余下部分作为绿化地,若设路宽为x cm.
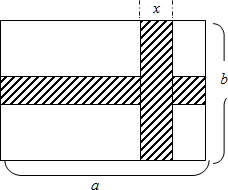 如图所示,在长为a cm,宽为b cm的长方形地面上修两条同样宽的道路,余下部分作为绿化地,若设路宽为x cm.
如图所示,在长为a cm,宽为b cm的长方形地面上修两条同样宽的道路,余下部分作为绿化地,若设路宽为x cm.