题目内容
(2002•重庆)如图,AB是⊙O的直径,四边形ABCD内接于⊙O,弧BC,弧CD,弧AD的度数比为3:2:4,MN是⊙O的切线,C是切点,则∠BCM的度数为 度.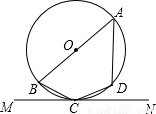
【答案】分析:连接OC,则∠OCM=90°,由弧BC,弧CD,弧AD的度数比为3:2:4,可求∠BOC=60°;又因为OB=OC,可求得∠OBC=∠OCB= (180°-∠BOC)=
(180°-∠BOC)= (180°-60°)=60°,即可求∠BCM=∠OCM-∠OCB=90°-60°=30°.
(180°-60°)=60°,即可求∠BCM=∠OCM-∠OCB=90°-60°=30°.
解答: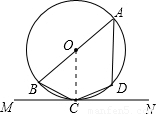 解:连接OC,
解:连接OC,
则∠OCM=90°,
∵弧BC、弧CD、弧AD的度数比为3:2:4;
设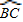 =3x,则
=3x,则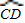 =2x,
=2x,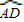 =4x,
=4x,
∵ +
+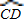 +
+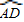 =180°,
=180°,
即3x+2x+4x=180°,
解得x=20°,3x=60°,即∠BOC=60°,
∵OB=OC,
∴∠OBC=∠OCB= (180°-∠BOC)=
(180°-∠BOC)= (180°-60°)=60°,
(180°-60°)=60°,
∠BCM=∠OCM-∠OCB=90°-60°=30°.
点评:本题考查了切线的性质及圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
 (180°-∠BOC)=
(180°-∠BOC)= (180°-60°)=60°,即可求∠BCM=∠OCM-∠OCB=90°-60°=30°.
(180°-60°)=60°,即可求∠BCM=∠OCM-∠OCB=90°-60°=30°.解答:
 解:连接OC,
解:连接OC,则∠OCM=90°,
∵弧BC、弧CD、弧AD的度数比为3:2:4;
设
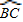 =3x,则
=3x,则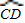 =2x,
=2x,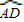 =4x,
=4x,∵
 +
+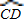 +
+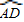 =180°,
=180°,即3x+2x+4x=180°,
解得x=20°,3x=60°,即∠BOC=60°,
∵OB=OC,
∴∠OBC=∠OCB=
 (180°-∠BOC)=
(180°-∠BOC)= (180°-60°)=60°,
(180°-60°)=60°,∠BCM=∠OCM-∠OCB=90°-60°=30°.
点评:本题考查了切线的性质及圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目