题目内容
18、已知，点A（x1，y1），B（x2，y2）在抛物y=tx2+2tx+4（0＜t＜3）上，x1＜x2，x1+x2=1-t，则y1与y2的大小关系是y1
＜
y2．分析：将点A，B分别代入抛物线方程，将y2与y1作差，差值用x1，x2与t表示，根据题设条件，判断差值正负号．
解答：解：分别将A，B的坐标代入抛物线方程得：
y1=tx12+2tx1+4
y2=tx22+2tx2+4
∴y2-y1=t（x22-x12）+2t（x2-x1）
=t（x2-x1）（x2+x1）+2t（x2-x1）
=t（1-t）（x2-x1）+2t（x2-x1）
=t（3-t）（x2-x1）
∵t＞0，3-t＞0，x2-x1＞0
∴y2-y1＞0
即：y2＞y1．
y1=tx12+2tx1+4
y2=tx22+2tx2+4
∴y2-y1=t（x22-x12）+2t（x2-x1）
=t（x2-x1）（x2+x1）+2t（x2-x1）
=t（1-t）（x2-x1）+2t（x2-x1）
=t（3-t）（x2-x1）
∵t＞0，3-t＞0，x2-x1＞0
∴y2-y1＞0
即：y2＞y1．
点评：理解点在抛物线上的含义，比较大小时先找出两个未知量的差值，再根据题设条件判断差值的符号，从而比较两个未知量的大小．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
已知三点P1（x1，y1），P2（x2，y2），P3（1，-2）都在反比例函数y=
的图象上，若x1＜0，x2＞0，则下列式子正确的是（ ）
| k |
| x |
| A、y1＜y2＜0 |
| B、y1＜0＜y2 |
| C、y1＞y2＞0 |
| D、y1＞0＞y2 |
已知：点A（x1，y1）、B（x2，y2）、C（x3，y3）是函数y=-
图象上的三点，且x1＜0＜x2＜x3则y1、y2、y3的大小关系是（ ）
| 3 |
| x |
| A、y1＜y2＜y3 |
| B、y2＜y3＜y1 |
| C、y3＜y2＜y1 |
| D、无法确定 |
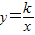的图象上，若x1＜0，x2＞0，则下列式子正确的是（ ）