题目内容
如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
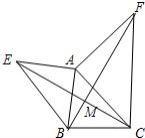
求证:(1)EC=BF;(2)EC⊥BF.
见解析
【解析】分析:首先根据角之间的关系推出∠EAC=∠BAF.再根据边角边定理,证明△EAC≌ △BAF.最后根据全等三角形的性质定理,得知EC=BF.根据角的转换可求出EC⊥BF.
证明:(1)因为 AE⊥AB,AF⊥AC,所以 ∠EAB=90°=∠FAC,
所以 ∠EAB+∠BAC=∠FAC+∠BAC.
又因为 ∠EAC=∠EAB+∠BAC,∠BAF=∠FAC+∠BAC.
所以 ∠EAC=∠BAF.
在△EAC与△BAF中,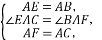
所以 △EAC≌△BAF. 所以 EC=BF.
(2)因为 ∠AEB+∠ABE=90°,又由△EAC≌△BAF可知∠AEC=∠ABF,
所以 ∠CEB+∠ABF+∠EBA=90°,即∠MEB+∠EBM=90°,即∠EMB=90°,
所以 EC⊥BF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案甲、乙两名学生进行射击练习,两人在相同条件下各射靶5次,射击成绩统计如下:
命中环数(单位:环) | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 2 | 2 | 0 | 1 |
乙命中相应环数的次数 | 1 | 3 | 1 | 0 |
从射击成绩的平均数评价甲、乙两人的射击水平,则( )
A.甲比乙高 B.甲、乙相同 C.乙比甲高 D.不能确定
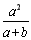
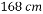
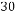
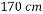
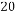
 ,然后从
,然后从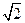 ,1,-1中选取一个你认为
,1,-1中选取一个你认为