题目内容
“移项”、“合并”、“系数化为1”都是将一个比较复杂的一元一次方程如2x-19=7x+31,变形成一个最简单的一元一次方程如x=-10.你能将方程ax+b=cx+d(x未知,a、b、c、d已知,且a≠c)化成最简单的一元一次方程吗?分析:只要按照“移项”、“合并”、“系数化为1”的步骤进行计算即可.
解答:解:能,
移项得:ax-cx=d-b,
合并得:(a-c)x=d-b,
∵a≠c,
∴系数化为1得:x=
.
移项得:ax-cx=d-b,
合并得:(a-c)x=d-b,
∵a≠c,
∴系数化为1得:x=
| d-b |
| a-c |
点评:本题考查了含有字母参数的一元一次方程的解法,其实质与一般的一元一次方程的解法一致,但要注意:系数不能为0.

练习册系列答案
相关题目
解方程
[
(x+1)+4]=3
+
变形第一步较好的方法是( )
| 3 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| 2x |
| 3 |
| A、去分母 | B、去括号 |
| C、移项 | D、合并同类项 |

 =2-
=2-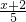 ”
”