题目内容
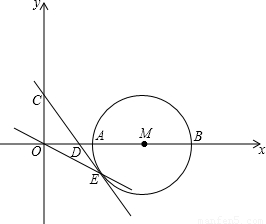
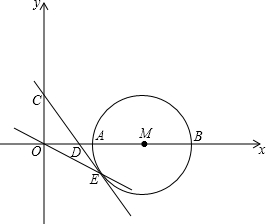
如图示已知点M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴 于A、B,抛物线
于A、B,抛物线 过A、B两点且与y轴交于点C.
过A、B两点且与y轴交于点C.
(1)求点C的坐标并画出抛物线的大致图象;
(2)已知点Q(8,m),P为抛物线对称轴上一动点,求出P点坐标使得PQ+PB值最小,并求出最小值;
(3)过C点作⊙M的切线CE,求直线OE的解析式.
解:(1)将A(2,0)B(6,0)代入 中,得:
中,得:
 ,
,
解得 ;
;
∴ ;
;
将x=0代入上式,则y=2,
∴C(0,2).

(2)将x=8代入抛物线的解析式中,得y=2,
∴Q(8,2);
过Q作QK⊥x轴,
过对称轴直线x=4作B的对称点A,则PB+PQ=QA;
在Rt△AQK中,AQ= =
= =
=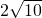 ,
,
即PB+PQ=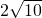 ;
;
已知直线AQ:y= x-
x- ,
,
当x=4时,y= ,故P(4,
,故P(4, ).
).
(3)如图有CE1和CE2,连接CM;
在Rt△COM和Rt△ME1C中 ,
,
∴Rt△COM≌Rt△MEC(HL);
则有矩形COME1,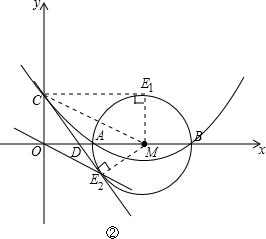
则E1点坐标为(4,2);
有直线OE1解析式为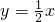 ,
,
连接ME2、OE2
在△COD和△ME2D中,
∵ ,
,
∴△COD≌△ME2D(AAS),
则OD=E2D,DC=DM,
∴∠DOE2=∠DE2O,∠DCM=∠DMC,
∵∠ODE2=∠CDM,
∴∠DOE2=∠DE2O,∠DCM=∠DMC,
则CM与OE2平行;
设CM的解析式为y=kx+b,则有:
 ,
,
解得 ;
;
∴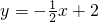 ;
;
则OE2的解析式为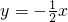 .
.
分析:(1)根据圆心M的坐标和圆的半径,即可得到A、B两点的坐标,将它们代入抛物线的解析式中,即可求得待定系数的值,进而可确定该抛物线的解析式,即可得到点C的坐标.
(2)由于点Q在抛物线的图象上,将其代入抛物线的解析式中,即可确定点Q的坐标,由于A、B关于抛物线的对称轴对称,那么AQ与抛物线对称轴的对称点即为所求的P点,先求出直线AQ的解析式,联立抛物线的对称轴,即可得到点Q的坐标;而PQ+PB的最小值即为AQ的长,已知A、Q的坐标,即可利用勾股定理求得AQ的长,由此得解.
(3)此题应分两种情况考虑:
①E点在M点上方,此时易证得四边形OCE1M是矩形,根据点M的坐标和圆的半径即可得到点E1的坐标,进而可利用待定系数法求得直线OE1的解析式;
②E点在M点下方,由于CO=ME2=2,易证得△COD≌△ME2D,可得OD=DE2,CD=DM,那么∠DOE2=∠DE2O=∠DCM=∠DMC,由此可证得CM∥OE2,可先求出直线CM的斜率,进而可求出直线OE2的解析式.
点评:此题主要考查了二次函数解析式的确定、平面展开-最短路径问题、全等三角形的判定和性质等重要知识点,同时还考查了分类讨论的数学思想,难度较大.
 中,得:
中,得: ,
,解得
 ;
;∴
 ;
;将x=0代入上式,则y=2,
∴C(0,2).

(2)将x=8代入抛物线的解析式中,得y=2,
∴Q(8,2);
过Q作QK⊥x轴,
过对称轴直线x=4作B的对称点A,则PB+PQ=QA;
在Rt△AQK中,AQ=
 =
= =
=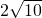 ,
,即PB+PQ=
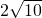 ;
;已知直线AQ:y=
 x-
x- ,
,当x=4时,y=
 ,故P(4,
,故P(4, ).
).(3)如图有CE1和CE2,连接CM;
在Rt△COM和Rt△ME1C中
 ,
,∴Rt△COM≌Rt△MEC(HL);
则有矩形COME1,

则E1点坐标为(4,2);
有直线OE1解析式为
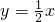 ,
,连接ME2、OE2
在△COD和△ME2D中,
∵
 ,
,∴△COD≌△ME2D(AAS),
则OD=E2D,DC=DM,
∴∠DOE2=∠DE2O,∠DCM=∠DMC,
∵∠ODE2=∠CDM,
∴∠DOE2=∠DE2O,∠DCM=∠DMC,
则CM与OE2平行;
设CM的解析式为y=kx+b,则有:
 ,
,解得
 ;
;∴
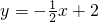 ;
;则OE2的解析式为
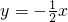 .
.分析:(1)根据圆心M的坐标和圆的半径,即可得到A、B两点的坐标,将它们代入抛物线的解析式中,即可求得待定系数的值,进而可确定该抛物线的解析式,即可得到点C的坐标.
(2)由于点Q在抛物线的图象上,将其代入抛物线的解析式中,即可确定点Q的坐标,由于A、B关于抛物线的对称轴对称,那么AQ与抛物线对称轴的对称点即为所求的P点,先求出直线AQ的解析式,联立抛物线的对称轴,即可得到点Q的坐标;而PQ+PB的最小值即为AQ的长,已知A、Q的坐标,即可利用勾股定理求得AQ的长,由此得解.
(3)此题应分两种情况考虑:
①E点在M点上方,此时易证得四边形OCE1M是矩形,根据点M的坐标和圆的半径即可得到点E1的坐标,进而可利用待定系数法求得直线OE1的解析式;
②E点在M点下方,由于CO=ME2=2,易证得△COD≌△ME2D,可得OD=DE2,CD=DM,那么∠DOE2=∠DE2O=∠DCM=∠DMC,由此可证得CM∥OE2,可先求出直线CM的斜率,进而可求出直线OE2的解析式.
点评:此题主要考查了二次函数解析式的确定、平面展开-最短路径问题、全等三角形的判定和性质等重要知识点,同时还考查了分类讨论的数学思想,难度较大.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 于A、B,抛物线
于A、B,抛物线 过A、B两点且与y轴交于点C.
过A、B两点且与y轴交于点C.
 过A、B两点且与y轴交于点C.
过A、B两点且与y轴交于点C.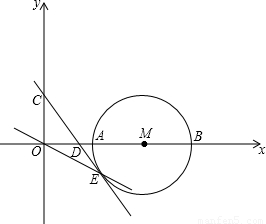
 过A、B两点且与y轴交于点C.
过A、B两点且与y轴交于点C.