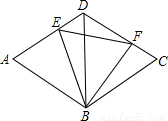
题目内容
如图,已知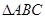 为等边三角形,
为等边三角形, 、
、 、
、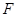 分别在边
分别在边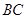 、
、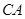 、
、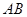 上,且
上,且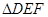 也是等边三角形.
也是等边三角形.
(1)除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的;
(2)你所证明相等的线段,可以通过怎样的变化相互得到?写出变化过程.

(1)AE=BF=CD,AF=BD=CE,证明见解析(2)线段AE、BF、CD它们绕△ABC的内心按顺时针(或按逆时针)方向旋转120°,可互相得到,线段AF、BD、CE它们绕△ABC的内心按顺时针(或按逆时针)方向旋转120°,可互相得到,变化过程见解析
【解析】解:(1)图中还有相等的线段是:AE=BF=CD,AF=BD=CE 2分
事实上,∵△ABC与△DEF都是等边三角形,
∴∠A=∠B=∠C=60°,∠EDF=∠DEF=∠EFD=60°,DE=EF=FD 3分
又∵∠CED+∠AEF=120°,∠CDE+∠CED=120°
∴∠AEF=∠CDE,同理,得∠CDE=∠BFD, 4分
∴△AEF≌△BFD≌△CDE(AAS),
所以AE=BF=CD,AF=BD=CE 5分
(2)线段AE、BF、CD它们绕△ABC的内心按顺时针(或按逆时针)方向旋转120°,可互相得到,线段AF、BD、CE它们绕△ABC的内心按顺时针(或按逆时针)方向旋转120°,可互相得到。 7分
由已知条件,根据等边三角形的性质推出△AEF≌△BFD≌△CDE.从而推出AE=BF=CD,AF=BD=CE.



 ,则等边三角
,则等边三角
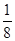 B.
B.  C.
C.
 D.1
D.1