题目内容
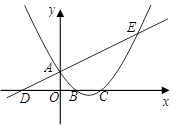
(本小题满分12分)已知:直线与
轴交于A,与
轴交于D,抛物线
与直线交于A、E两点,与
轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
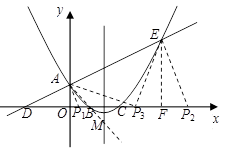
(2)动点P在![]() 轴上移动,当△PAE是直角三角形时,求点P的坐标.
轴上移动,当△PAE是直角三角形时,求点P的坐标.
(3)在抛物线的对称轴上找一点M,使的值最大,求出点M的坐标.
解:(1)将A(0,1)、B(1,0)坐标代入得
解得
∴抛物线的解折式为.
(2)设点E的横坐标为m,则它的纵坐标为
则E(,
).
又∵点E在直线上,
∴.
 解得
解得(舍去),
.
∴E的坐标为(4,3).
(Ⅰ)当A为直角顶点时
过A作交
轴于
点,设
.
易知D点坐标为(,0).
由得
即
,∴
.
∴.
(Ⅱ)同理,当为直角顶点时,
点坐标为(
,0).)
(Ⅲ)当P为直角顶点时,过E作轴于
,设
.
由,得
.
.
由得
.
解得,
.
∴此时的点的坐标为(1,0)或(3,0).
综上所述,满足条件的点P的坐标为(,0)或(1,0)或(3,0)或(
,0)
(3)抛物线的对称轴为.
∵B、C关于对称,
∴.
要使最大,即是使
最大.
由三角形两边之差小于第三边得,当A、B、M在同一直线上时的值最大.
易知直线AB的解折式为.
∴由 得
∴M(
,-
).
解析:略

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题:


 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线


