题目内容
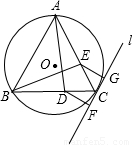
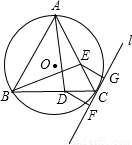
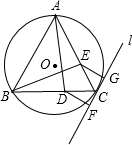如图，给定锐角三角形ABC，BC＜CA，AD，BE是它的两条高，过点C作△ABC的外接圆的切线l，过点D，E分别作l的垂线，垂足分别为F，G．试比较线段DF和EG的大小，并证明你的结论．
分析：由于l是切线，利用弦切角定理可得∠FCD=∠EAB，而∠DFC=∠BEA=90°，可证Rt△FCD∽Rt△EAB，那么
有
=
，同理可得EG=AD•
，∠ACB既在△BCE，又在△ACD中，那么易得tan∠ACB=
=
，即BE•CD=AD•CE，从而可证DF=EG．
有
| DF |
| CD |
| BE |
| AB |
| CE |
| AB |
| AD |
| CD |
| BE |
| CE |
解答：解：结论是DF=EG．
∵∠FCD=∠EAB，∠DFC=∠BEA=90°，
∴Rt△FCD∽Rt△EAB，
∴
=
，
∴DF=BE•
，
同理可得EG=AD•
，
又∵tan∠ACB=
=
，
∴BE•CD=AD•CE，
∴DF=EG．
∵∠FCD=∠EAB，∠DFC=∠BEA=90°，
∴Rt△FCD∽Rt△EAB，
∴
| DF |
| CD |
| BE |
| AB |
∴DF=BE•
| CD |
| AB |
同理可得EG=AD•
| CE |
| AB |
又∵tan∠ACB=
| AD |
| CD |
| BE |
| CE |
∴BE•CD=AD•CE，
∴DF=EG．
点评：本题利用了弦切角定理、相似三角形的判定和性质、正切概念．
练习册系列答案
相关题目
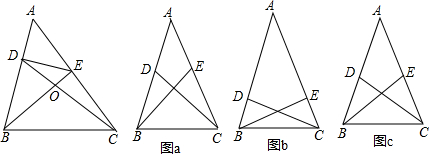
∠A，BE与CD相交于点O，探究BD与CE之间的数量关系，并证明你的结论．
