题目内容
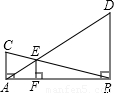
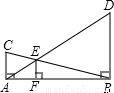
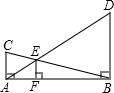 如图,两个有公共直角的Rt△ABC和Rt△ABD的斜边交于点E,EF⊥AB,垂足为F,若AC=4cm,BD=12cm,则EF的长为________.
如图,两个有公共直角的Rt△ABC和Rt△ABD的斜边交于点E,EF⊥AB,垂足为F,若AC=4cm,BD=12cm,则EF的长为________.
3cm
分析:由题意可得出AC∥BD,所以,∠C=∠DBE,∠CAE=∠D,即由相似三角形的判定定理可以得出△AEC∽△DEB,所以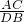 =
= =
= ,同理可得:△AEF∽△ADB,由相似三角形的性质可得
,同理可得:△AEF∽△ADB,由相似三角形的性质可得 =
=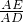 =
= ,代入BD的值求出EF即可.
,代入BD的值求出EF即可.
解答:如上图所示:
∵∠CAB=∠DBA=90°,即:CA⊥AB,DB⊥AB
∴AC∥BD
∴∠C=∠DBE,∠CAE=∠D
∴△AEC∽△DEB
∴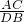 =
= =
=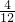 =
=
又EF⊥AB,DB⊥AB
同理可得:△AEF∽△ADB
∴ =
=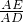 =
= =
= =
=
∴EF= ×BD=
×BD= ×12=3cm.
×12=3cm.
点评:本题主要考查相似三角形的判定与性质,关键在于找出条件判断两个三角形相似,并利用相似三角形的相应的性质求解.
分析:由题意可得出AC∥BD,所以,∠C=∠DBE,∠CAE=∠D,即由相似三角形的判定定理可以得出△AEC∽△DEB,所以
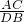 =
= =
= ,同理可得:△AEF∽△ADB,由相似三角形的性质可得
,同理可得:△AEF∽△ADB,由相似三角形的性质可得 =
=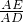 =
= ,代入BD的值求出EF即可.
,代入BD的值求出EF即可.解答:如上图所示:
∵∠CAB=∠DBA=90°,即:CA⊥AB,DB⊥AB
∴AC∥BD
∴∠C=∠DBE,∠CAE=∠D
∴△AEC∽△DEB
∴
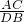 =
= =
=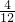 =
=
又EF⊥AB,DB⊥AB
同理可得:△AEF∽△ADB
∴
 =
=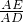 =
= =
= =
=
∴EF=
 ×BD=
×BD= ×12=3cm.
×12=3cm.点评:本题主要考查相似三角形的判定与性质,关键在于找出条件判断两个三角形相似,并利用相似三角形的相应的性质求解.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
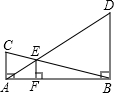 如图,两个有公共直角的Rt△ABC和Rt△ABD的斜边交于点E,EF⊥AB,垂足为F,若AC=4cm,BD=12cm,则EF的长为
如图,两个有公共直角的Rt△ABC和Rt△ABD的斜边交于点E,EF⊥AB,垂足为F,若AC=4cm,BD=12cm,则EF的长为