题目内容
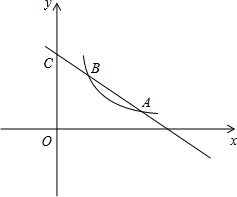 如图,函数y1=k1+b与函数y2=
如图,函数y1=k1+b与函数y2=| k2 | x |
(1)求函数y1、y2的表达式及点B的坐标;
(2)观察图象比较当x>0时,y1和y2的大小.
分析:(1)先根据点A(2,1)在反比例函数的图象上求出k2的值,进而可得出反比例函数的解析式;再由AC两点均在一次函数的图象上求出k1、b的值,进而可得出一次函数的解析式;把一次函数与反比例函数的解析式联立,即可得出B点坐标;
(2)直接根据AB两点的坐标即可得出当x>0时,y1和y2的大小.
(2)直接根据AB两点的坐标即可得出当x>0时,y1和y2的大小.
解答:解:(1)∵点A(2,1)在反比例函数y2=
的图象上,
∴k2=2×1=2,
∴反比例函数y2=
的解析式为:y2=
;
∵A(2,1),C(0,3)在一次函数y1=k1x+b的图象上,
∴
,解得
,
∴一次函数的解析式为:y1=-x+3;
∴
,解得
或
,
∴B(1,2);
(2)∵A(2,1),B(1,2),
∴当0<x<1或x>2时,反比例函数的图象在一次函数图象的上方,即y2>y1;
当1<x<2时,y1>y2;
当x=1或x=2时,y1=y2.
| k2 |
| x |
∴k2=2×1=2,
∴反比例函数y2=
| k2 |
| x |
| 2 |
| x |
∵A(2,1),C(0,3)在一次函数y1=k1x+b的图象上,
∴
|
|
∴一次函数的解析式为:y1=-x+3;
∴
|
|
|
∴B(1,2);
(2)∵A(2,1),B(1,2),
∴当0<x<1或x>2时,反比例函数的图象在一次函数图象的上方,即y2>y1;
当1<x<2时,y1>y2;
当x=1或x=2时,y1=y2.
点评:本题考查的是反比例函数与一次函数的交点问题,涉及到用待定系数法求一次函数及反比例函数的解析式及利用数形结合求不等式的解集,根据题意得出B点坐标是解答此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
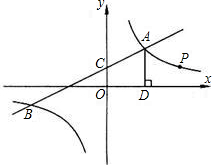 ,-2),与y轴交于点C.
,-2),与y轴交于点C.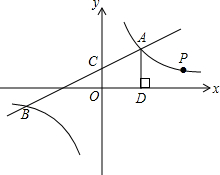 如图,一次函数y1=k1x+2与反比例函数y2=
如图,一次函数y1=k1x+2与反比例函数y2=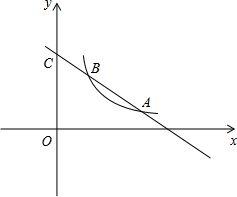 如图,函数y1=k1+b与函数y2=
如图,函数y1=k1+b与函数y2=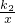 的图象(x>0)交于A、B两点,与y轴交于点C,已知点A的坐标为(2,1),点C的坐标为(0,3)
的图象(x>0)交于A、B两点,与y轴交于点C,已知点A的坐标为(2,1),点C的坐标为(0,3)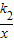 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C