题目内容
已知半径为4和 的两圆相交,公共弦长为4,则两圆的圆心距为 .
的两圆相交,公共弦长为4,则两圆的圆心距为 .
【答案】分析:设⊙O1的半径为r=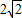 ,⊙2的半径为R=4,公共弦为AB,两圆的圆心的连线与公共弦的交点为C;那么根据相交两圆的定理,可出现来两个直角三角形,△O1AC和△O2AC,再利用勾股定理可求出O1C和O2C,就可求出O1O2.
,⊙2的半径为R=4,公共弦为AB,两圆的圆心的连线与公共弦的交点为C;那么根据相交两圆的定理,可出现来两个直角三角形,△O1AC和△O2AC,再利用勾股定理可求出O1C和O2C,就可求出O1O2.
解答: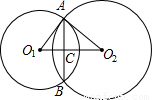 解:在Rt△O1AC中,O1C=
解:在Rt△O1AC中,O1C=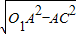 =
=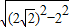 =2,
=2,
同理,在Rt△O2AC中,O2C=2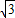 ,
,
∴O1O2=O1C+O2C=2+2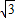 .
.
还有一种情况,O1O2=O2C-O1C=2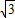 -2.
-2.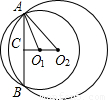
点评:本题利用了相交两圆的定理,还用了勾股定理.
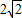 ,⊙2的半径为R=4,公共弦为AB,两圆的圆心的连线与公共弦的交点为C;那么根据相交两圆的定理,可出现来两个直角三角形,△O1AC和△O2AC,再利用勾股定理可求出O1C和O2C,就可求出O1O2.
,⊙2的半径为R=4,公共弦为AB,两圆的圆心的连线与公共弦的交点为C;那么根据相交两圆的定理,可出现来两个直角三角形,△O1AC和△O2AC,再利用勾股定理可求出O1C和O2C,就可求出O1O2.解答:
 解:在Rt△O1AC中,O1C=
解:在Rt△O1AC中,O1C=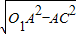 =
=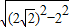 =2,
=2,同理,在Rt△O2AC中,O2C=2
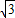 ,
,∴O1O2=O1C+O2C=2+2
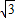 .
.还有一种情况,O1O2=O2C-O1C=2
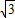 -2.
-2.
点评:本题利用了相交两圆的定理,还用了勾股定理.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 的两圆相交,公共弦长为4,则两圆的圆心距为________.
的两圆相交,公共弦长为4,则两圆的圆心距为________.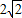 的两圆相交,公共弦长为4,则两圆的圆心距为 .
的两圆相交,公共弦长为4,则两圆的圆心距为 . 的两圆相交,公共弦长为4,则两圆的圆心距为 .
的两圆相交,公共弦长为4,则两圆的圆心距为 .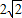 的两圆相交,公共弦长为4,则两圆的圆心距为 .
的两圆相交,公共弦长为4,则两圆的圆心距为 .