题目内容
(2004•泉州)某施工队修建一个抛物线形的水泥门洞,其高度OM为8米,地面宽度AB为12米,在门洞中搭一个“三角架”CDE.使C点在门洞的左侧,D为OB的中点,CE⊥AB于E,以AB所在直线为x轴,AB的中点O为原点建立直角坐标系(如图所示)(1)请你直接写出A、B、M三点的坐标;
(2)现测得DE=7米,求“三角架”的高CE.

【答案】分析:(1)根据抛物线在坐标系的位置,可直接写出A,B,M三点的坐标;
(2)由于抛物线的对称轴是y轴,设解析式y=ax2+8,用待定系数法求a,确定解析式,在对解析式进行实际应用.
解答:解:(1)A(-6,0)、B(6,0)、M(0,8);
(2)根据抛物线在坐标系的位置设解析式:y=ax2+8
把B(6,0)代入得a=-
∴y=- x2+8
x2+8
当DE=7时,由AB为12米,AB的中点O,
∴OB= AB=6米,
AB=6米,
又∵O为OB的中点,
则OD=3米,
∴OE=4,即E(-4,0)
把x=-4代入y=- x2+8,
x2+8,
得y=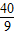
即CE=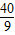 米.
米.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
(2)由于抛物线的对称轴是y轴,设解析式y=ax2+8,用待定系数法求a,确定解析式,在对解析式进行实际应用.
解答:解:(1)A(-6,0)、B(6,0)、M(0,8);
(2)根据抛物线在坐标系的位置设解析式:y=ax2+8
把B(6,0)代入得a=-

∴y=-
 x2+8
x2+8当DE=7时,由AB为12米,AB的中点O,
∴OB=
 AB=6米,
AB=6米,又∵O为OB的中点,
则OD=3米,
∴OE=4,即E(-4,0)
把x=-4代入y=-
 x2+8,
x2+8,得y=
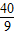
即CE=
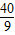 米.
米.点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目


