题目内容
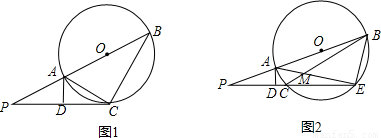
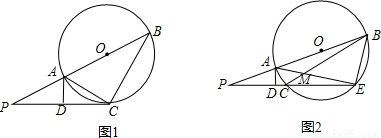
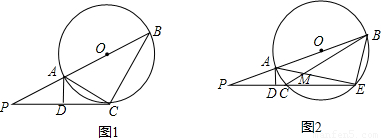
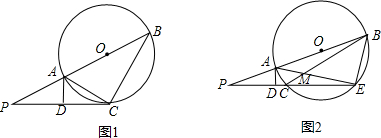
如图①,线段PB过圆心O,交圆O于A、B两 点,PC切圆O于点C,作AD⊥PC,垂足为D,连接AC、BC。(1)写出图①中所有相等的角(直角除外),并给出证明;
(2)若图①中的切线PC变为图②中割线PCN的情形,PCN与圆O交于C、N两点,AN与BC交于点M,AD⊥PN,写出图②中相等的角(写出三组即可,直角除外);
(3)在图②中,证明AD·AB=AC·AN。
(2)若图①中的切线PC变为图②中割线PCN的情形,PCN与圆O交于C、N两点,AN与BC交于点M,AD⊥PN,写出图②中相等的角(写出三组即可,直角除外);
(3)在图②中,证明AD·AB=AC·AN。

解:(1)图①中相等的角有:
∠ACD=∠ABC,∠BAC=∠CAD,
证明:连接OC,则OC⊥PC,
∵AD⊥PC,
∴AD∥OC,
∴∠CAD=∠OCA,
又OA=OC,∠BAC=∠OCA,
∴∠BAC=∠CAD,
又AB为直径,∠ACB=90°,
∴∠BAC+∠B=90°,
∴∠CAD+∠ACD=90°,
∴∠ACD=∠ABC;
(2)∠ACD=∠ABN,∠ABC=∠ANC,∠BAN=∠BCN,∠BNA=∠BCA,∠CBN=∠CAN(三组即可)。(3)易证△ADC≌△ANB,
∴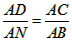 ,
,
∴AD·AB=AC·AN。
∠ACD=∠ABC,∠BAC=∠CAD,
证明:连接OC,则OC⊥PC,
∵AD⊥PC,
∴AD∥OC,
∴∠CAD=∠OCA,
又OA=OC,∠BAC=∠OCA,
∴∠BAC=∠CAD,
又AB为直径,∠ACB=90°,
∴∠BAC+∠B=90°,
∴∠CAD+∠ACD=90°,
∴∠ACD=∠ABC;
(2)∠ACD=∠ABN,∠ABC=∠ANC,∠BAN=∠BCN,∠BNA=∠BCA,∠CBN=∠CAN(三组即可)。(3)易证△ADC≌△ANB,
∴
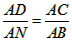 ,
,∴AD·AB=AC·AN。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);
点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);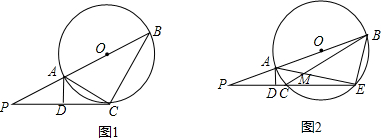 点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);
点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);