Question

抛物线y=ax²与直线x=1，x=2，y=1，y=2围成的正方形有公共点，则实数a的取值范围是（　　）

• A、

  1

  4

  ≤a≤1
• B、

  1

  2

  ≤a≤2
• C、

  1

  2

  ≤a≤1
• D、

  1

  4

  ≤a≤2

Answer 1

分析：此题主要考数形结合，画出图形找出范围，问题就好解决了．

解答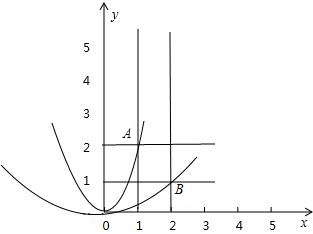：解：由右图知：A（1，2），B（2，1），
再根据抛物线的性质，|a|越大开口越小，
把A点代入y=ax²得a=2，
把B点代入y=ax²得a=

1

4

，
则a的范围介于这两点之间，故

1

4

≤a≤2．
故选D．

点评：此题考查学生的观察能力，把函数性质与正方形连接起来，要学会数形结合．