题目内容
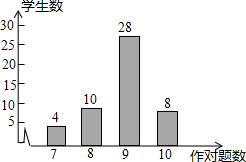
 某校九年级进行了一次数学测验,本次测验共有10道题目.为了解学生本次测验做对题目的数量情况,数学老师从中随机抽查了部分学生的试卷,并绘制成条形统计图.结合统计图,可得以下结论:
某校九年级进行了一次数学测验,本次测验共有10道题目.为了解学生本次测验做对题目的数量情况,数学老师从中随机抽查了部分学生的试卷,并绘制成条形统计图.结合统计图,可得以下结论:①被抽查学生的做对题数是该问题的一个样本,样本中的数据有50个;
②样本数据的中位数是9,众数是28;
③样本数据的极差是24;
④本次数学测验全年级学生平均做对了约8.8道题.
其中正确结论的序号是
①④
①④
.分析:①每组数据的个数的和就是样本中数据的个数;
②根据中位数与众数定义即可作出判断;
③极差就是最大值与最小值的差,根据定义即可求解;
④利用加权平均数公式即可求解.
②根据中位数与众数定义即可作出判断;
③极差就是最大值与最小值的差,根据定义即可求解;
④利用加权平均数公式即可求解.
解答:解:①样本中的数据有:4+10+28+8=50,故命题正确;
②样本数据的中位数是9,众数是9,故命题错误;
③样本数据的极差是:10-7=3,故命题错误;
④次数学测验全年级学生平均作对题数是:
=8.8,故命题正确.
故答案是:①④.
②样本数据的中位数是9,众数是9,故命题错误;
③样本数据的极差是:10-7=3,故命题错误;
④次数学测验全年级学生平均作对题数是:
| 4×7+10×8+28×9+8×10 |
| 50 |
故答案是:①④.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数、众数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据量的数.给定一组数据,出现次数最多的那个数,称为这组数据的众数.

练习册系列答案
相关题目
 某校九年级进行了一次数学测验,本次测验共有10道题目.为了解学生本次测验做对题目的数量情况,数学老师从中随机抽查了部分学生的试卷,并绘制成条形统计图.结合统计图,可得以下结论:
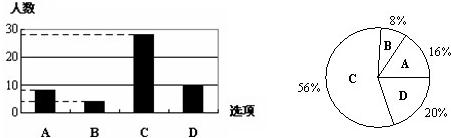
某校九年级进行了一次数学测验,本次测验共有10道题目.为了解学生本次测验做对题目的数量情况,数学老师从中随机抽查了部分学生的试卷,并绘制成条形统计图.结合统计图,可得以下结论: 某校九年级进行了一次消防安全知识测验,本次测验共有10道选择题.为了解学生在本次测验中答对题目的数量情况,老师从中随机抽查了部分学生的试卷,并根据这些试卷的答对题数绘制成如下条形统计图.由图可知,这10道选择题全都正确的学生人数占总人数的百分率是________.
某校九年级进行了一次消防安全知识测验,本次测验共有10道选择题.为了解学生在本次测验中答对题目的数量情况,老师从中随机抽查了部分学生的试卷,并根据这些试卷的答对题数绘制成如下条形统计图.由图可知,这10道选择题全都正确的学生人数占总人数的百分率是________.