题目内容
19、如图，平面上有四个点A、B、C、D，根据下列语句画图（1）画直线AB； 作射线BC；画线段CD；
（2）连接AD，并将其反向延长至E，使DE=2AD；
（3）找到一点F，使点F到A、B、C、D四点距离和最短．
分析：根据直线向两方无限延伸；射线向一方无限延伸；线段有两个端点画出图形即可．
解答：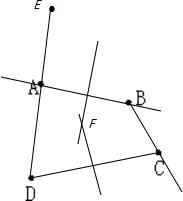
解：（1）过AB作直线即可；
以点B为顶点，作过点C的射线即可得到射线BC；
连接CD，即可得到线段CD．
（2）连接AD，并将其反向延长至E，使DE=2AD即可；
（3）连接AB、CD，作线段AB、CD的垂直平分线，两条垂直平分线的交点即为P点．
解：（1）过AB作直线即可；以点B为顶点，作过点C的射线即可得到射线BC；
连接CD，即可得到线段CD．
（2）连接AD，并将其反向延长至E，使DE=2AD即可；
（3）连接AB、CD，作线段AB、CD的垂直平分线，两条垂直平分线的交点即为P点．
点评：本题考查的是直线、射线、线段的定义及性质，解答此题的关键是熟知以下知识，即直线向两方无限延伸；射线向一方无限延伸；线段有两个端点画出图形即可．
练习册系列答案
相关题目
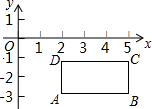如图，平面上有四个点，它们的坐标分别是A（2，-2
如图，平面上有四个点A、B、C、D，按下列要求画出图形：（不写作法，保留作图痕迹）
画图题：
如图，平面上有四个点A，B，C，D，按下列要求画出图形．