题目内容
 按要求完成作图,并回答问题:如图三角形ABC中
按要求完成作图,并回答问题:如图三角形ABC中(1)画线段BC的中点D,并连接AD;
(2)过点A画BC的垂线,垂足为E;
(3)根据上述作图,若∠ABC=60°,则∠BAE=
(4)用“<”、“=”、“>”填空:AB+AC
分析:利用圆的性质作出BC的中点,再利用三角形内角和定理解答.
解答:解:(1)分别以B,C为圆心,大于
BC为半径画圆,两圆相交于F,过F作FD⊥BC于D,
则点D即为BC的中点;
(2)过点A画BC的垂线,垂足为E;
(3)∵在△ABE中,∠ABC=60°,∠AEB=90°,
∴∠BAE=180°-60°-30°=30°,BD=2cm,
则BC=2BD=4cm;
(4)AB+AC>BC,根据两点之间,线段最短.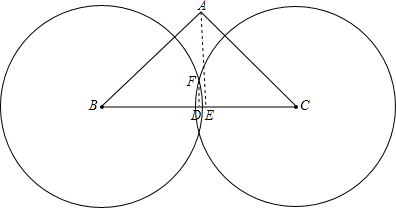
| 1 |
| 2 |
则点D即为BC的中点;
(2)过点A画BC的垂线,垂足为E;
(3)∵在△ABE中,∠ABC=60°,∠AEB=90°,
∴∠BAE=180°-60°-30°=30°,BD=2cm,
则BC=2BD=4cm;
(4)AB+AC>BC,根据两点之间,线段最短.

点评:本题考查了同学们对圆的掌握情况,体现了圆在尺规作图中的重要作用.同时考查了三角形的性质定理,是中学阶段的重点.

练习册系列答案
相关题目
 按要求完成作图,并回答问题;如图在△ABC中:
按要求完成作图,并回答问题;如图在△ABC中: 23、按要求完成作图,并回答问题;如图在△ABC中:
23、按要求完成作图,并回答问题;如图在△ABC中: 按要求完成作图,并回答问题:如图三角形ABC中
按要求完成作图,并回答问题:如图三角形ABC中