题目内容
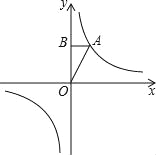
【题目】如图,已知反比例函数y=![]() (k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1.
(k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1.
(1)求m,k的值;
(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y=![]() 的图象有两个不同的公共点,求实数n的取值范围.
的图象有两个不同的公共点,求实数n的取值范围.
【答案】(1)、m=2;k=2;(2)、:n>﹣![]() 且n≠0
且n≠0
【解析】
试题分析:(1)、根据三角形的面积公式即可求得m的值;(2)、若一次函数y=nx+2(n≠0)的图象与反比例函数y=![]() 的图象有两个不同的公共点,则方程
的图象有两个不同的公共点,则方程![]() =nx+2有两个不同的解,利用根的判别式即可求解.
=nx+2有两个不同的解,利用根的判别式即可求解.
试题解析:(1)、由已知得:S△AOB=![]() ×1×m=1, 解得:m=2,
×1×m=1, 解得:m=2,
把A(1,2)代入反比例函数解析式得:k=2;
(2)、由(1)知反比例函数解析式是y=![]() ,
,
由题意得: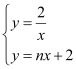 有两个不同的解,即
有两个不同的解,即![]() =nx+2有两个不同的解, 方程去分母,得:nx2+2x﹣2=0,
=nx+2有两个不同的解, 方程去分母,得:nx2+2x﹣2=0,
则△=4+8n>0, 解得:n>﹣![]() 且n≠0.
且n≠0.

练习册系列答案
相关题目
【题目】某鞋店试销一款女鞋,试销期间对不同颜色鞋的销售情况统计如下表:
颜色 | 黑色 | 棕色 | 白色 | 红色 |
销售量(双) | 60 | 50 | 10 | 15 |
鞋店经理最关心的是哪种颜色的鞋最畅销,则对鞋店经理最有意义的统计量是( )
A. 平均数B. 众数C. 中位数D. 方差