题目内容
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )
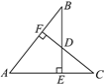
A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
【答案】D
【解析】
由题, BE⊥AC于E,CF⊥AB于F,∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A, 在Rt△AFC中∠C=90°-∠A,∴∠B=∠C,在△ABE和△ACF中,∠A=∠A, AB = AC,∠B=∠C,∴△ABE≌△ACF(ASA),故A选项正确,∵△ABE≌△ACF,∴AE=AF,AC=AB,连接AD,在Rt△AFD和Rt△AED中, AE=AF,AD=AD,∴Rt△AFD≌Rt△AED(HL),∠DAF=∠DAE,即点D在∠BAC的平分线上,选项B正确,由AE=AF,AC=AB,得BF=CE,在△BDF和△CDE中,∠BFD=∠CED=90°,∠B=∠C, BF=CE,∴△BDF≌△CDE,选项C正确,而点D不一定是BE的中点,故选D.
试题全等三角形的判定方法有:1.边边边(SSS);2.边角边(SAS);3.角角边(AAS);4.角边角(ASA);5.直角三角形中的斜边直角边(HL);两三角形全等,对应边相等,对应角相等,由题, BE⊥AC于E,CF⊥AB于F,∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A, 在Rt△AFC中∠C=90°-∠A,∴∠B=∠C,在△ABE和△ACF中,∠A=∠A, AB = AC,∠B=∠C,∴△ABE≌△ACF(ASA),故A选项正确,∵△ABE≌△ACF,∴AE=AF,AC=AB,连接AD,在Rt△AFD和Rt△AED中, AE=AF,AD=AD,∴Rt△AFD≌Rt△AED(HL),∠DAF=∠DAE,即点D在∠BAC的平分线上,选项B正确,由AE=AF,AC=AB,得BF=CE,在△BDF和△CDE中,∠BFD=∠CED=90°,∠B=∠C, BF=CE,∴△BDF≌△CDE,选项C正确,而点D不一定是BE的中点,故选D.

【题目】2019年7月9日,北京市滴滴快车调整了价格,规定车费由“总里程费+总时长费”两部分构成,具体收费标准如下表:(注:如果车费不足起步价,则按起步价收费.)
时间段 | 里程费(元/千米) | 时长费(元/分钟) | 起步价(元) |
06:00—10:00 | 1.80 | 0.80 | 14.00 |
10:00—17:00 | 1.45 | 0.40 | 13.00 |
17:00—21:00 | 1.50 | 0.80 | 14.00 |
21:00—06:00 | 2.15 | 0.80 | 14.00 |
(1)小明07:10乘快车上学,行驶里程6千米,时长10分钟,应付车费 元;
(2)小芳17:20乘快车回家,行驶里程1千米,时长15分钟,应付车费 元;
(3)小华晚自习后乘快车回家,20:45在学校上车.由于道路施工,车辆行驶缓慢,15分钟后选择另外道路,改道后速度是改道前速度的3倍,10分钟后到家,共付了车费37.4元,问从学校到小华家快车行驶了多少千米?
【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟) | 0 | 10 | … | 25 |
水池的容积V(公升) | 100 | 300 | … | 600 |
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
【题目】为了迎接浙江省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
A绳子 | B绳子 | C绳子 | |
长度(米) | 8 | 6 | 4 |
单价(元/条) | 12 | 8 | 6 |
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.