题目内容
已知y1=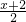
，y2=
；
（1）当x取何值时，y1=y2；
（2）当x取何值时，y1比y2小2．
解：根据题意得：
（1）y1=y2，即=，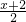
化简可得：3（x+2）=2（x-1），
解得：x=-8；
（2）y1比y2小2，即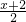=-2，
化简可得：3（x+2）=2（x-1）-12，
解得：x=-20．
分析：根据题意得到一元一次方程，解即可．
点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果；
（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．
（1）y1=y2，即
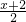=，化简可得：3（x+2）=2（x-1），
解得：x=-8；
（2）y1比y2小2，即
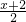=-2，化简可得：3（x+2）=2（x-1）-12，
解得：x=-20．
分析：根据题意得到一元一次方程，解即可．
点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果；
（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．
练习册系列答案
相关题目
已知y1=a1x2+b1x+c1，y2=a2x2+b2x+c2且满足
=
=
=k(k≠0，1)．则称抛物线y1，y2互为“友好抛物线”，则下列关于“友好抛物线”的说法不正确的是（ ）
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| A、y1，y2开口方向、开口大小不一定相同 |
| B、因为y1，y2的对称轴相同 |
| C、如果y2的最值为m，则y1的最值为km |
| D、如果y2与x轴的两交点间距离为d，则y1与x轴的两交点间距离为|k|d |
，那么S2与
之间的大小关系是
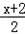，y2=