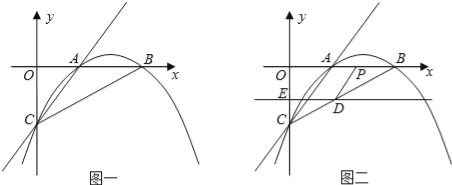
��Ŀ����
����Ŀ����ͼ��������y=![]() x2+3��x�ύ�ڵ�A����B����ֱ��y=
x2+3��x�ύ�ڵ�A����B����ֱ��y=![]() x+b�ཻ�ڵ�B����C��ֱ��y=
x+b�ཻ�ڵ�B����C��ֱ��y=![]() x+b��y�ύ�ڵ�E��
x+b��y�ύ�ڵ�E��
��1��д��ֱ��BC�Ľ���ʽ��
��2������ABC�������
��3������M���߶�AB����ÿ��1����λ���ȵ��ٶȴ�A��B�˶�������A��B�غϣ���ͬʱ����N������BC����ÿ��2����λ���ȵ��ٶȴ�B��C�˶������˶�ʱ��Ϊt�룬��д����MNB�����S��t�ĺ�����ϵʽ���������M�˶�����ʱ��ʱ����MNB���������������Ƕ��٣�
���𰸡���1��BC�Ľ���ʽΪy=![]() x+
x+![]() ��
��
��2��![]() ��4��
��4��![]() =
=![]()
��3������M�˶�2��ʱ����MNB������ﵽ������Ϊ![]() ��
��
��������
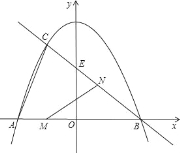
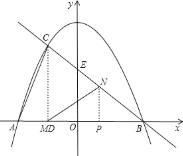
�����������1����y=0����y=-![]() x2+3�����A��B�����꣮��B���������y=-
x2+3�����A��B�����꣮��B���������y=-![]() x+b���BC�Ľ���ʽ��
x+b���BC�Ľ���ʽ��
��2���������������B��C�����꣮���AB��CD�ij�������������ABC�������
��3����N����NP��MB��֤����BNP�ס�BEO������֪��y=0�����E�����꣬�����߶α����NP��BE�ij������S��t�ĺ�����ϵʽ�����ö��κ������������S�����ֵ��
�����������1����y=-![]() x2+3����y=0����-
x2+3����y=0����-![]() x2+3=0����x1=2��x2=��2
x2+3=0����x1=2��x2=��2
��A����2��0����B��2��0�����ֵ�B��y=-![]() x+b�ϣ���0=-
x+b�ϣ���0=-![]() +b��b=
+b��b=![]()
��BC�Ľ���ʽΪy=-![]() x+
x+![]() ����
����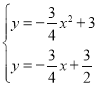 ����
���� ��
��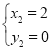 ��
��
��C(-1��![]() )��B��2��0������AB=4��CD=
)��B��2��0������AB=4��CD=![]() ��
��
��![]() ��4��
��4��![]() =
=![]() ������N��NP��MB�ڵ�P����EO��MB����NP��EO
������N��NP��MB�ڵ�P����EO��MB����NP��EO
���BNP�ס�BEO����![]() ����ֱ��y=-
����ֱ��y=-![]() x+
x+![]() �ɵã�E(0,
�ɵã�E(0,![]() )
)
������BEO��BO=2��EO=![]() ����BE=
����BE=![]() ����
����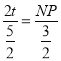 ����NP=
����NP=![]() t����S=
t����S=![]() .
.![]() t����4��t��=��
t����4��t��=��![]() t2+
t2+![]() t��0��t��4��=��
t��0��t��4��=��![]() ��t��2��2+
��t��2��2+![]()
���������߿������£�
����t=2ʱ��S���=![]() ��������M�˶�2��ʱ����MNB������ﵽ������Ϊ
��������M�˶�2��ʱ����MNB������ﵽ������Ϊ![]() ��
��

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д� �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�