题目内容
 已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.
已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.
求证:AP平分∠BPC.
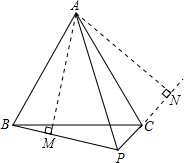 证明:过点A作AM⊥BP,AN⊥PN,交PC的延长线于点N,
证明:过点A作AM⊥BP,AN⊥PN,交PC的延长线于点N,可得出∠AMB=∠ANC=90°,
∵∠ACN+∠ACP=180°,且∠ABM+∠ACP=180°,
∴∠ACN=∠ABM,
又△ABC是等边三角形,
∴AB=AC,
在△ABM和△ACN中,
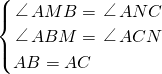 ,
,∴△ABM≌△ACN(AAS),
∴AM=AN,又AM⊥BP,AN⊥PN,
∴PA平分∠BPC.
分析:过点A作AM⊥BP,AN⊥PN,交PC的延长线于点N,利用垂直的定义得到一对直角相等,由邻补角定义得到∠ACN+∠ACP=180°,又∠ABM+∠ACP=180°,可得出一对角相等,再由三角形ABC为等边三角形,得到AB=AC,利用AAS可得出△ABM≌△ACN,利用全等三角形的对应边相等得到AM=AN,由在角内部,到角两边距离相等的点一定在角的平分线上,可得出PA为∠BPC的平分线.
点评:此题考查了等边三角形的性质,全等三角形的判定与性质,以及角平分线的逆定理,作出两条垂线,构造全等直角三角形是解本题的关键.

练习册系列答案
相关题目
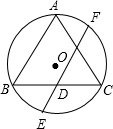 已知如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥BA,若⊙O的半径为
已知如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥BA,若⊙O的半径为4
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 22、已知如图,△ABC是等腰直角三角形,∠C为直角.
22、已知如图,△ABC是等腰直角三角形,∠C为直角. 已知如图,△ABC是等边三角形,E、G是AB边的三等分点,F、H是AC边的三等分点,则图中阴影部分的面积是△ABC的面积的( )
已知如图,△ABC是等边三角形,E、G是AB边的三等分点,F、H是AC边的三等分点,则图中阴影部分的面积是△ABC的面积的( ) 已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.
已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.