题目内容
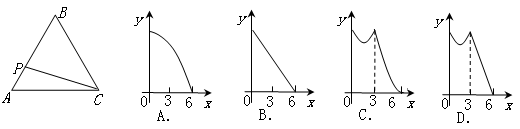
已知抛物线 经过点A(-1,0),B(3,0),交
经过点A(-1,0),B(3,0),交 轴于点C,M为抛物线的顶点,连接MB.
轴于点C,M为抛物线的顶点,连接MB.

(1)求该抛物线的解析式;
(2)在 轴上是否存在点P满足△PBM是直角三角形,若存在,请求出P点的坐标,若不存在,请说明理由;
轴上是否存在点P满足△PBM是直角三角形,若存在,请求出P点的坐标,若不存在,请说明理由;
(3)设Q点的坐标为(8,0),将该抛物线绕点Q旋转180°后,点M的对应点为 ,求
,求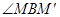 的度数.
的度数.
 经过点A(-1,0),B(3,0),交
经过点A(-1,0),B(3,0),交 轴于点C,M为抛物线的顶点,连接MB.
轴于点C,M为抛物线的顶点,连接MB.
(1)求该抛物线的解析式;
(2)在
 轴上是否存在点P满足△PBM是直角三角形,若存在,请求出P点的坐标,若不存在,请说明理由;
轴上是否存在点P满足△PBM是直角三角形,若存在,请求出P点的坐标,若不存在,请说明理由;(3)设Q点的坐标为(8,0),将该抛物线绕点Q旋转180°后,点M的对应点为
 ,求
,求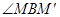 的度数.
的度数.(1)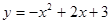 (2)P点的坐标为(0,1),(0,3),
(2)P点的坐标为(0,1),(0,3), ,
,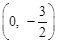
(3) =135°
=135°
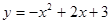 (2)P点的坐标为(0,1),(0,3),
(2)P点的坐标为(0,1),(0,3), ,
,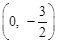
(3)
 =135°
=135°试题分析:(1)∵因为抛物线
 经过点A(-1,0),B(3,0)
经过点A(-1,0),B(3,0)∴
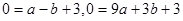
解得
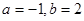
∴
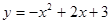
(2)设点P的坐标为(0,y),
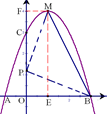
① 若∠MPB=90°,过点M作ME ⊥x轴,MF ⊥y轴,
易证R t △PFM ∽ R t △BOP,可得:
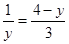
解得
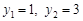 ,∴点P的坐标为(0,1),(0,3)
,∴点P的坐标为(0,1),(0,3)
② 若∠PMB=90°,同理,R t △PFM ∽ R t △BEM,
∴
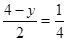 解得:
解得: ∴点P的坐标为
∴点P的坐标为 
③ 若∠MBP=90°,同理, R t △POB ∽ R t △BEM
∴
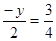 ,解得:
,解得: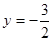 ,∴点P的坐标为
,∴点P的坐标为 
综上:△PBM是直角三角形时,P点的坐标为(0,1),(0,3),
 ,
,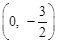
(3)
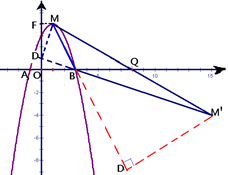
由题意可知:B(3,0),M(1,4),Q(8,0),点M,M′关于点Q中心对称,
∴M′ (15,-4),
连结M′B,并延长M′B交y轴于点D,
由
 ,可得D(0,1)
,可得D(0,1)连结MD,易证R t △DFM≌R t △DOB
∴△DBM是等腰直角三角形,∠DBM=45°
∴
 =135°
=135°解法二:
过点M′作MB的垂线交MB的延长线于点D,
由△MBM′面积计算,转化为已知△面积和底边MB求高D M′,解得
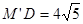
再由
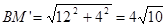 , M’D⊥MD, ∴△DBM′是等腰Rt△,
, M’D⊥MD, ∴△DBM′是等腰Rt△,∴

∴ ∠M’BD=∠BM’D=45°
∴
 =135°
=135°点评:该题较为复杂,是常考题,主要考查学生对求二次函数解析式以及对图形中点与线段在直角坐标系中表示的方法的应用。

练习册系列答案
相关题目
 与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
 的图象过点
的图象过点 .
.
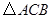 是直角三角形;
是直角三角形; 在第二象限,且是抛物线上的一动点,过点
在第二象限,且是抛物线上的一动点,过点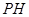 垂直
垂直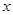 轴于点
轴于点 ,试探究是否存在以
,试探究是否存在以 为顶点的三角形与
为顶点的三角形与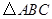 相似?若存在,求出
相似?若存在,求出 ,在平面直角坐标系中,等腰直角
,在平面直角坐标系中,等腰直角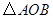 的斜边
的斜边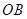 在
在 轴上,顶点
轴上,顶点 的坐标为
的坐标为 ,
,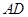 为斜边上的高.抛物线
为斜边上的高.抛物线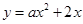 与直线
与直线 交于点
交于点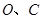 ,点
,点 的横坐标为
的横坐标为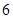 .点
.点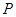 在
在 轴.交射线
轴.交射线 于点
于点 .设点
.设点 ,以
,以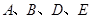 为顶点的四边形的面积为
为顶点的四边形的面积为 .
.
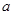 的值;
的值;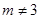 时,求
时,求 ,设直线
,设直线 交射线
交射线 于点
于点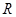 ,交抛物线于点
,交抛物线于点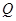 .以
.以 为一边,在
为一边,在 ,其中
,其中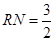 .直接写出矩形
.直接写出矩形 的图象如图所示,则一次函数
的图象如图所示,则一次函数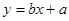 的图象不经过( ).
的图象不经过( ).
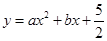 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.