题目内容
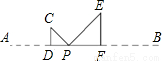
已知:点P为线段AB上的动点(与A、B两点不重合).在同一平面内,把线段AP、BP分别折成△CDP、△EFP,其中∠CDP=∠EFP=90°,且D、P、F三点共线,如图所示.

(1)若△CDP、△EFP均为等腰三角形,且DF=2,求AB的长;
(2)若AB=12,tan∠C=![]() ,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值.
,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值.
答案:
解析:
解析:
|
(1)设 (2)连结CE.
由于 因此分两种情况考虑. 当∠DCP=∠PEF时, 设 根据勾股定理,可得 当 设 根据勾股定理,可得 综上所述,四边形CDFE的面积的最小值为6.…………8分 |

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
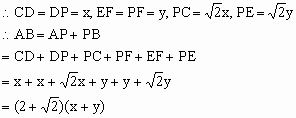
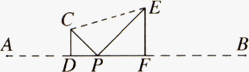
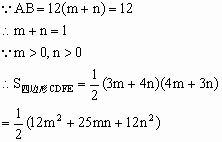
 (2007•海淀区二模)已知:点P为线段AB上的动点(与A、B两点不重合).在同一平面内,把线段AP、BP分别折成△CDP、△EFP,其中∠CDP=∠EFP=90°,且D、P、F三点共线,如图所示.
(2007•海淀区二模)已知:点P为线段AB上的动点(与A、B两点不重合).在同一平面内,把线段AP、BP分别折成△CDP、△EFP,其中∠CDP=∠EFP=90°,且D、P、F三点共线,如图所示.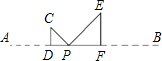
 ,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值.
,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值.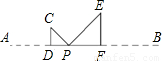
 ,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值.
,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值.