题目内容
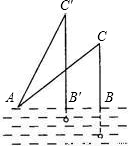
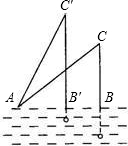 如图,钓鱼竿AC长6m,露在水面上的鱼线BC长3
如图,钓鱼竿AC长6m,露在水面上的鱼线BC长3| 2 |
| 3 |
| A、60° | B、45° |
| C、15° | D、90° |
分析:因为三角形ABC和三角形AB′C′均为直角三角形,且BC、B′C′都是我们所要求角的对边,所以根据正弦来解题,分别求出∠CAB,∠C'AB',然后可以求出∠C'AC,即求出了鱼竿转过的角度.
解答:解:∵sin∠CAB=
=
=
,
∴∠CAB=45°.
∵sin∠C′AB′=
=
=
,
∴∠C′AB′=60°.
∴∠CAC′=60-45=15°,
鱼竿转过的角度是15°.
故选C.
| BC |
| AC |
3
| ||
| 6 |
| ||
| 2 |
∴∠CAB=45°.
∵sin∠C′AB′=
| B′C′ |
| AC |
3
| ||
| 6 |
| ||
| 2 |
∴∠C′AB′=60°.
∴∠CAC′=60-45=15°,
鱼竿转过的角度是15°.
故选C.
点评:此题中BC、B′C′都是我们所要求角的对边,而AC是斜边,所以本题利用了正弦的定义.解本题的关键是把实际问题转化为数学问题.

练习册系列答案
相关题目
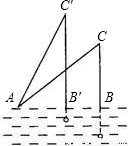 如图,钓鱼竿AC长6m,露在水面上的鱼线BC长
如图,钓鱼竿AC长6m,露在水面上的鱼线BC长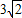 m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为
m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为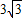 ,则鱼竿转过的角度是( )
,则鱼竿转过的角度是( )A.60°
B.45°
C.15°
D.90°
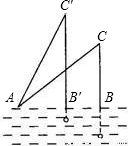 如图,钓鱼竿AC长6m,露在水面上的鱼线BC长
如图,钓鱼竿AC长6m,露在水面上的鱼线BC长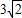 m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为
m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为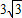 ,则鱼竿转过的角度是( )
,则鱼竿转过的角度是( )A.60°
B.45°
C.15°
D.90°
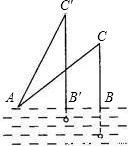 如图,钓鱼竿AC长6m,露在水面上的鱼线BC长
如图,钓鱼竿AC长6m,露在水面上的鱼线BC长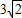 m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为
m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为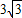 ,则鱼竿转过的角度是( )
,则鱼竿转过的角度是( )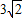 m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为
m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C为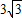 ,则鱼竿转过的角度是( )
,则鱼竿转过的角度是( )