题目内容
 把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD=( )
把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD=( )分析:根据折叠性质得出∠EBC=∠ABC,求出∠MBD=∠EBD,推出∠CBD=∠CBE+∠DBE=
(∠ABE+∠EBM),代入求出即可.
| 1 |
| 2 |
解答:解:∵沿BC折叠A和E重合,
∴∠EBC=∠ABC,
∵BD平分∠EBM,
∴∠MBD=∠EBD,
∴∠CBD=∠CBE+∠DBE=
(∠ABE+∠EBM)=
×180°=90°,
故选D.
∴∠EBC=∠ABC,
∵BD平分∠EBM,
∴∠MBD=∠EBD,
∴∠CBD=∠CBE+∠DBE=
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查了折叠性质,角平分线,角的计算的应用,关键是推出∠CBD=
∠ABM.
| 1 |
| 2 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
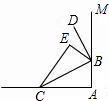 如图,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD=
如图,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD= 把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD=
把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD= 如图,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD=________.
如图,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,则∠CBD=________.