题目内容
已知△ABC是等腰三角形，BC=8，AB，AC的长是关于x的一元二次方程x2﹣10x+k=0的两根，则（ ）
| A．k="16" | B．k=25 |
| C．k=﹣16或k=﹣25 | D．k=16或k=25 |
C.
试题分析：根据当BC是腰，则AB或AC有一个是8，进而得出k的值，再利用当BC是底，则AB和AC是腰，再利用根的判别式求出即可．
当BC是腰，则AB或AC有一个是8，故82-10×8+k=0，
解得：k=-16，
当BC是底，则AB和AC是腰，则b2-4ac=102-4×1×k=100-4k=0，
解得：k=-25，
综上所述：k=-16或k=-25．
故选：C．
考点: 一元二次方程的应用．
练习册系列答案
一线名师提优试卷系列答案
相关题目
；
＝
,∠A=30°,求∠B的度数
的两个根为
那么
．
的根是（ ）．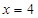
，
，
，
